Se împlinesc mai bine de 7 ani de când am adăugat pe blog primele articole despre metodele de rezolvare a problemelor de matematică. Atunci, la început de ciclu primar al lui Andrei, eram încă în rolul de părinte disperat și de rubrică s-a ocupat în mare măsură tatăl meu. Se ocupă și în continuare, căci copiii caută pe net, adaugă probleme, iar articolele la care am colaborat cu el au un număr impresionant de comentarii de-a lungul timpului. Odată cu a doua mea specializare, am preluat în parte scrierea articolelor, iar zilele trecute l-am refăcut un pic pe primul, cel dedicat metodei figurative, pentru a-l putea recomanda câtorva părinți care se străduiesc să își susțină copilul acasă, dar (mi se pare normal, că doar nu au studii de specialitate) nu prea știu cum.
Cu această ocazie am constatat că articolul nu includea explicația unei probleme atunci când datele cunoscute includ diferența și raportul dintre necunoscutele problemei. Se dă, așadar, următoarea problemă:
Ana are într-un coș de răchită mere galbene și roșii. Numărul merelor galbene este de 4 ori mai mare decât al merelor roșii, iar diferența este 24. Câte mere galbene are Ana? Dar mere roșii? Rezolvați folosind metoda figurativă.
Primul pas ce trebuie făcut este analiza datelor problemei. Experiența îmi arată că copiii nu citesc cu atenție cerințele și în loc de a rumega datele, îl iau pe „nu știu” în brațe, aleargă la prima persoană adultă care, cum altfel, de multe ori îi scutește de treabă, și se amăgește cu răspunsul copilului că „a înțeles”.
Ne sunt utile toate informațiile din problemă?
Nu. Nu ne interesează că merele sunt în coș, sau că e coșul din răchită. Este o informație inutilă în rezolvarea acesteia.
Ce informații ne oferă problema?
- Avem două necunoscute, mere galbene (g) și mere roșii (r).
- Știm că mere galbene sunt mai multe decât mere roșii.
- Cunoaștem diferența între numărul merelor galbene și roșii.
Care sunt cuvintele cheie ale problemei?
- „de 4 ori mai mare”, ceea ce înseamnă o operație de înmulțire: 4 x r = g
- „diferența este 24”, ceea ce înseamnă o operație de scădere: g – r = 24
Dacă copilul ajunge la aceste expresii matematice, este tentat să continue rezolvarea fără să apeleze la metoda figurativă. Însă avem o cerință în acest sens…
Vom începe cu realizarea desenului. Avem două necunoscute, mere galbene și roșii, așadar desenul nostru va cuprinde două segmente, unul mai mic și unul mai mare, căci nu avem același număr de mere de culori diferite.
Am stabilit că merele roșii sunt cele mai puține, așadar primul segment, mai mic, va reprezenta merele roșii. Al doilea segment, mai mare – merele galbene. De câte ori va fi mai mare al doilea segment? De 4 ori. Așadar desenăm al doilea segment având lungimea de 4 ori mai mare decât a primului. Recomand ca aceste rezolvări, cel puțin la început, să fie realizate pe foi cu pătrățele. Desenăm primul segment de 3 pătrățele, al doilea va avea: 3 x4 = 12 (pătrățele). Însă dacă vă doriți ca copilul să participe la concursuri de excelență, învățați-l să lucreze pe foaie velină. Desenezi cu rigla un segment de 2 cm. Următorul va avea 2 x 4 = 8 cm.
În construcție se poate proceda la desenarea celui de-al doilea segment multiplicându-l pe primul. Se desenează dedesubt, pornind dintr-un punct aliniat cu primul, un segment identic, apoi se continuă adăugarea a încă trei segmente de aceeași dimensiune, rezultând un segment de patru ori mai mare decât primul (alcătuit din patru părți de dimensiunea primului).
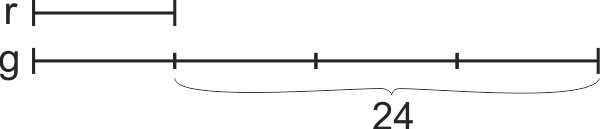
Din problemă cunoaștem „diferența”. Dacă comparăm cele două segmente desenate, care este „diferența” între ele? Ce are în plus al doilea față de primul? Sau – dacă din al doilea îl scădem / dăm la o parte pe primul, cu ce rămânem? Am constatat că aici au existat dificultăți mari în înțelegere, însă sunt convinsă că, lucrând la clasele mai mici cu material concret în învățarea operațiilor matematice, aceste dificultăți pot fi reduse.
Revenind la analiza desenului: din câte părți egale este format al doilea segment, care reprezintă merele galbene? Din 4 părți egale, căci este de patru ori mai mare decât primul segment. Câte din aceste părți egale reprezintă ce are „în plus” față de primul, sau „diferența” dintre acesta și primul? 3 părți egale.
Dacă trei părți egale reprezintă 24, cât este o parte?
24 : 3 = 8 (o parte egală, în problema noastră: numărul merelor roșii)
Câte mere galbene avem?
8 x 4 = 32 (mere galbene), dacă folosim informația potrivit căreia sunt „de patru ori mai multe”,
sau: 8 + 24 = 32 (mere galbene), dacă ne folosim de diferența dintre ele.
La răspuns notăm R: 32, 8., răspunzând, în ordinea în care au fost puse, la întrebările problemei.
Nu uităm de verificare. La această etapă trebuie să folosim datele obținute ca răspuns pentru a ajunge la datele problemei. Nu vom efectua așadar 32+8=40, pentru că problema nu ne spune câte mere sunt în total. Avem ca alternativă 32-8=24 (verificăm diferența), sau 32 : 8 = 4.
Tatăl meu încheia articolele cu o temă, însă sunt convinsă că ați ajuns la acest articol căutând ajutor pe google pentru o anumită problemă din multitudinea de culegeri pe care le avem. Dacă aveți în continuare nevoie de ajutor în rezolvare, vă rog să țineți cont și de mesajul de mai jos:
Important!
Nu adăuga probleme fără a menționa în ce clasă ești(este copilul) și neaparat cum te-ai gândit tu să rezolvi problema. Nu rezolvăm aici temele elevilor, doar îi ajutăm în cazul în care s-au împotmolit la rezolvare.
Mesajele care conțin doar cerințele problemei vor fi (probabil) ignorate.