În săptămânile ce urmează voi prezenta, la nivel de clasa a IV-a, trei metode de rezolvare a problemelor de matematică: metoda figurativă (grafică), metoda comparaţiei şi metoda mersului invers.
Atunci când rezolvăm probleme de matematică trebuie să avem în vedere următoarele: întâi de toate, înţelegerea problemei şi exprimarea în limbaj matematic a relaţiilor dintre mărimile care apar în textul acesteia.
Mă refer la următoarele formulări, care dețin, de cele mai multe ori, cheia rezolvării unei probleme:
- Expresia *cu atât mai mult* înseamnă o adunare;
- Expresia *cu atât mai puţin* înseamnă o scădere;
- Expresia *de atâtea ori mai mult* înseamnă o înmulţire;
- Expresia *de atâtea ori mai puţin* înseamnă o împărţire.
Următoarele exprimări sunt folosite destul de des în culegerile matematice. Sunt însă de evitat, dat fiind faptul că un „număr” nu poate fi „mărit”, cel mult putem afla un alt număr care este „mai mare cu…” decât numărul ales. Însă ele apar, și e bine să le cunoașteți.
*măriţi cu 2 numărul X* X+2;
*micşoraţi cu 2 numărul X*, X-2;
*măriţi de 2 ori numărul A*, Ax2;
*micşoraţi de 2 ori numărul A*, A:2.
Atenţie mare așadar la exprimările ce apar în textul problemelor! Dacă întâlniți asemenea expresii, este util să notați deasupra lor semnul operației matematice pe care o indică, vor ușura rezolvarea.
De regulă, atunci când avem de rezolvat o problemă, încercăm mai întâi să o încadrăm într-un anumit tip, pentru care cunoaștem un algoritm de rezolvare.
Voi prezenta acum rezolvarea unei probleme prin metoda figurativă. Esenţial în rezolvarea problemelor cu această metodă este realizarea unui desen, o figură, care corespunde enunţului dat.
Problemă: Un număr este cu 3 mai mare decât altul. Să se afle numerele, ştiind că suma lor este 25.
Rezolvare(I)
Din enunţ ne dăm seama că:
- nu cunoaştem 2 numere;
- unul dintre ele este cu 3 mai mare;
- suma celor 2 numere este 25.
Realizăm următorul desen:

Observăm că, dacă am elimina din suma numerelor 3, adică am lua din numărul mai mare 3 unităţi, cele două segmente desenate devin egale. Scopul acestei metode de rezolvare este acela de a obține pe desen un număr de părți egale, care să ne ajute apoi la identificarea necunoscutelor.
Vom scrie:
25-3=22, unde 22 reprezintă suma celor două numere, dacă al doilea ar fi egal cu primul.
Câte părți egale am obținut în desen, după ce am eliminat 3?
1+1 = 2 (părți egale)
Dacă suma a două părți egale este 22, putem afla cât reprezintă o parte egală, împărțind suma la numărul de părți egale identificate.
22: 2=11 (reprezintă o parte egală, în problema noastră aceasta reprezentând numărul mai mic.
Am aflat în acest mod numărul mai mic, celălalt poate fi aflat în două moduri. Ori adunăm unitățile îndepărtate inițial:
11+ 3= 14,
Sau scădem din sumă numărul pe care l-am aflat:
25-11=14.
În concluzie numerele sunt 11 şi 14, ceea ce se verifică uşor (11+14=25). Nu uitaţi, după ce aţi rezolvat o problemă, verificaţi întotdeauna rezultatul obţinut!
Rezolvare(II)
Se poate realiza şi următorul desen:
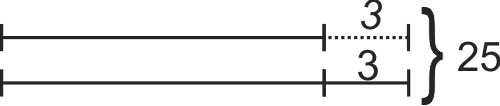
Observăm că, dacă am adăuga la numărul mai mic 3 unităţi, suma ar creşte cu 3 şi numerele devin egale. Obținem așadar două părți egale.
Vom scrie
25+ 3=28, unde 28 este suma numerelor, dacă primul ar fi egal cu al doilea.
Câte părți egale am obținut în desen, după ce am adăugat 3?
1+1 = 2 (părți egale)
Dacă suma a două părți egale este 28, putem afla cât reprezintă o parte egală, împărțind suma la numărul de părți egale identificate.
apoi
28: 2=14.
Am aflat în acest mod numărul mai mare. Celălalt poate fi aflat tot în două moduri. Ori eliminăm unitățile îndepărtate inițial:
14-3=11,
Sau scădem din suma inițială numărul pe care l-am aflat:
25-11=14
Deci, numerele sunt 11 şi 14, rezultate obţinute şi prin prima variantă de rezolvare.
În final aş atrage atenţia că nu este de ajuns să ştiu în ce constă metoda figurativă şi să rezolv o problemă, două… Fiecare problemă aduce un element de noutate şi trebuie să ne punem în cât mai multe situaţii, adică să rezolvăm cât mai multe, pentru a nu fi luaţi prin surprindere!
Temă:
1. Un număr este cu 10 mai mare decât altul. Aflaţi cele două numere, dacă suma lor este 40.
2. Un număr este de 3 ori mai mare decât altul. Aflaţi numerele, dacă suma lor este 40.
Important!
Nu posta probleme fără a menționa în ce clasă ești și neaparat cum te-ai gândit tu să rezolvi problema. Nu rezolvăm aici temele elevilor, doar îi ajutăm în cazul în care s-au împotmolit la rezolvare.
Mesajele care conțin doar cerințele problemei vor fi (probabil) ignorate.
- Operații cu puteri. Compararea puterilor - 4 decembrie 2020
- Matematica: ultima cifra a unui numar natural - 8 decembrie 2014
- Rezolvareaproblemelor cu ajutorul ecuatiilor si sistemelor de ecuatii - 10 februarie 2013



Buna seara !
Va rog sa ma ajutati la aceasta problema , daca se poate :
1. Die ABCD un tetraedru regulat cu muchia de 6 cm , in care notam cu M mijlocul muchiei [CD]. Calculati :
a) lungimea proiectiei segmentului [AB] pe planul ( BCD) ;
B) lungimea proiectiei segmentului [AM] pe planul [BCD].
Draga Antonia,
a)B apartine planului BCD; proiectia lui B pe planul BCD este B(1). Proiectia lui A pe planul BCD este centrul de greutate al triunghiului BCD; fie G acesta.(AG inaltimea tetraedrului)(2). Din 1 si 2 proiectia lui AB in planul BCD este BG.
b)M apartine planului BCD; proiectia lui M in planul BCD este M (3). Din 3 si 2 proiectia lui AM in planul BCD este MG. Cu bine.
Buna seara !
Va rog sa ma ajutati la aceste probleme , daca se poate :
1. Se da expresia E(x) = 5(x+1)²-(2x-3)² + ( 1-x)(x+1)
2. Fie VABCD o piramida patrulatera regulata. Daca inaltimea si apotema piramidei au lungimile de 2√2 cm , respectiv 3 cm , calculati perimetrul bazei ABCD.
Va multumesc !
Draga Antonia,
E(x)=5(x^2+2x+1)-(4x^2-12x+9)+(1-x^2)=5X^2+10x+5-4x^2+12x-9+1-x^2=22x-3.
Daca notam cu G centrul de greutate al bazei, VG inaltimea piramidei.M mijlocul laturii BC, VM apotema piramidei. Triunghiul VGM, dreptunghic in G, deoarece VG perpendiculara pe baza deci pe GM; aplicand teorema lui Pitagora, VM^2=VG^2+GM^2, obtinem 9=8+GM^2, adica GM^2=9-8=1 , de unde GM=1. Gm fiind apotema patratului, latura bazei este AB=2GM=2*1=2; perimetrul bazei este 4*2=8cm.Sper sa te descurci! Cu bine.
Buna ziua !
Va rog sa ma ajutati la aceste exercitii :
1. Calculati :
a) ( x-6/x+1 + 6x/x²+2x+1 ) x(inmultit) x+1/x-2
b) (x²+5x/x²-6x+9 – x+4/x-3) : x+3/x-3
2. Se da expresia E(x) = ( 1/x – 2/x² + 1/x³) x(inmultit) x² / x-1 :
a) Efectuati calculele pentru a obtine forma cea mai simpla a expresiei.
b) Rezolvati in Z ecuatia E(x)=2.
Draga Antonia,
Imi pare rau ca nu pot sa ti raspund, pentru ca se scriu greu fractiile aici. Se lucreaza la fel ca la numere rationale. Cu bine.
Buna seara !
Va rog sa ma ajutati la acest exercitiu :
1. Se considera multimile E={ m ∈ N / 2^m< 3²} si F={n ∈ N*/n=m-1, m ∈ E}
a) Determinati multimile E si F.
Va multumesc !
Draga Antonia,
2^0<9(A)
2^1<9(A)
2^2<9(A)
2^3<9(A)
2^4<9 (F). Pentru valori mai mari sau egale decat 4 obtinem propozitii false.E={0,1,2,3}.
m=0, n=0-1=-1
m=1, n=1-1=0
m=2, n=2-1=1
m=3, n=3-1=2. F={-1,0,1,2}
Buna seara !
Nu am prea inteles teorema celor 3 perpendiculare. Va rog sa ma ajutati la aceasta problema :
1.Fie AbCD un dreptunghi cu AB=4 cm si BC= 2 cm. In punctul B se construieste perpendiculara pe planul dreptunghiului pe care se considera punctul E astfel incat EB=2√2 cm. Calculati:
A) d(E,AD) ;
B) d(E,CD).
Draga Antonia,Sper ca ti ai construit figura! EB perpendiculara pe planul ABCD, EB perpendiculara pe BA, BA perpendiculara pe AD, Conform cu th celor 3 perpendiculare EA perpendiculara pe AD, deci EA este distanta de la E la AD; se calculeaza din triunghiul dreptunghic EBA cu th lui PItagora.Analog se face pentru EC. Cu bine.
Eu nu am inteles nimic din felul in care ati prezentat metoda figurativa .Un elev de clasa a lV a nici atat ….
Într-o gradinita cu flori sunt de 6 ori mai multe albine decat bondari. Daca zboara 6 albine si tot atatia bondari, numarul albinelor ramase este de 8 ori mai mare decat numarul bondarilor. Cate albine si cati bondari sunt in gradinita?
Draga Bianca,
Nu mi ai spus ce clasa esti! Fie x numarul albinelor, y numarul bondarilor. x=6y(1). Daca pleaca cate 6 din fiecare, vor ramane x-6 si y-6. De aici x-6=8(y-6)(2).Inlocuim 1 in 2 si obtinwm(3) 6y-6=8(y-6). Rezolvi ecuatia 3, afliy apoi x. Cu bine.
Buna seara ma numesc Andra sunt clasa a patra si va rog sa imi explicati sa pot rezolva aceasta problema daca se poate. Suma a doua numere este 64. Impartind numarul cel mare la cel mic obtinem catul 3 si restul 4 . Care sunt numerele.
Draga Andra,
/––/ numarul mai mic
/–-/–-/–-/+4 numarul mai mare. Suma lor 64. Scadem 4 si raman 4 parti egale.64-4=60. 60:4=15. Numarul mai mic este 15, iar cel mare 3.15+4=49.Cu bine.
Buna ziua sunt Timi clasa a4a daca ar face 20 de tractoare pe zi ar lipsi la termen 100 dde tractoare,daca ar face zilnic 23 de tractoare ar fi cu 20 mai mult decat comanda . Cate tractoare au fost comandate si in cate zile trebuia onorata comanda ?
Draga Timi,
Daca numarul zilelor ar fi n, atunci numarul tractoarelor ar fi in primul caz 20.n+100(1),iar in al doilea 23.n-20(2). Egalam 1 si 2 si obtinem
23n-20=20n+100. Adunam 20 in ambii membri si o btinem 23n+20-20=20n+100+20 sau 23n=20n+120, Scadem 20n din ambii membri si obtinem 23n-20n=20n–20n+120 sau 3n=120, de unde n=120:3 sau n=40 zile. Numarul tractoarelor este 20.40+100=800+100=900 sau 23.40-20=920-20=900. Cu bine.
PS. Citeste pe acest site si proprietati ale egalitatilor.
Va foarte multumesc . Parintele 🙂
Pentru a putea rezolva urmatoarele probleme va rog sa ne ajutati la una pentru model .
Daca ar fi cate 10 jucatori la fiecare panou raman 2 panouri libere .Daca ar fi cate 7 jucatori lanfiecare panou la ultimul ar mai trebui 2 jucatori .Cate panouri erau si cati jucatori?
Multumesc
x si y sunt nr intregi pentru care x+1 ori y+2 egal cu 3 sunt…… VA ROG AJUTATIMA URGENT
Draga Camelia,
3 se scrie ca produs 1.3,3.1,-1.(-3),-3.(-1).Punem pe rand x+1=1 si y+2=3 samd. Rezolvi opt ecuatii si gasesti toate val posibile. Cu bine.
Buna ziua ,ma puteti va rog ajuta cu urmatoarea problema ?
Suma a trei numere este 131. Primul este cu 23 mai mare decat al doilea, iar al treilea este cu 13 mai mare decat jumatatea celui de-al doilea.
|_____________________________|___23___|
|______________|______________|
|______________|__13____|
Aceasta este reprezentarea grafică. Continuati rezolvarea!
Buna ziua !
Va rog sa ma ajutati la aceasta problema :
1. Se considera prisma triunghiulara regulata ABCDA’B’C’D’ care are perimetrul bazei egal cu 6√6 cm si muchia laterala de 6 cm. Aflati :
a) masura unghiului dintre planele B’BC si A’AC. ( aici cred ca trebuie sa folosesc unghiul diedru) ;
b) aria triunghiului A’BC ;
c) distanta de la B’ la planul A’BC.
Va multumesc !
Draga Antonia,
E greu de scris rezolvarea acestei probleme! Cu bine!
Daca ma puteti ajuta la aceasta problema: Anul acesta varsta tatalui este de 4 ori mai mare decat a fiului, dar peste 20 de ani va fi de 2 ori mai mare. Cati ani va avea fiul peste 5 ani ?
Draga David,
/–/ varsta fiului
/–/–/–/–/ varsta tatalui, de 4 0ri mai mare. Dupa 20 de ani, vor avea
/–/+20, fiul
/–/–/–/–/+20, tatal.Acum varsta tatalui e de 2 ori mai mare decat a fiului, deci
/–/–/+20+20, am dublat varsta fiului. Observam ca 2 parti reprezinta 20 de ani. O parte va fi 20:2=10 ani are fiul.Peste 5 ani fiul are
10+5=…, te las pe tine sa faci adunarea. Cu bine.
Mersi mult Dani D. !
Cu placere! Te mai asteptam!!!
Buna ziua.
Suma a 3 nr este 96.primul este de trei ori mai mare decat al doilea,iar al treilea este egal cu diferenta dintre primul si al doilea.sa se afle nr
Prin segmente
Multumesc pt ajutor
Draga Dari,
/––/ al doilea numar
/––/––-/––-/ primul numar
/––/––/al treilea numar, diferenta primelor doua. Suma lor 96, 6 parti egale, afli o parte si apoi numerele. Cu bine.
Numarul 97 reprezinta suma a trei nr consecutive si nr 13.afla nr
Metoda reprezentarii grafice
Draga Dari,
Suma celor trei nr consecutive este 97-13=84
Daca cele trei nr sunt consecutive
/–––/
/––-/+1
/––-/+2. Suma lor 84. Scadem 3 si obtinem trei parti egale. 84-3=… O parte este…Cu bine. Sper sa te descurci!
Mama a adus acasa de 15 ori mai multe bomboane decat prajituri .Daca ar lua din bomboane 42 ,atunci bomboanele si prajiturile ramase ar fi in numar egal .Cate bomboane si cate prajituri sunt?
Draga Ana,
/–/ numarul prajiturilor
/–/–/–/–/–/–/–/–/–/–/–/–/–/–/–/numarul bomboanelor.Daca luam 42 de bomboane si nr prajiturilor ramane egal cu al bomboanelor, inseamna ca 14 parti reprezinta 42; deci o parte 42:14=3 bomboane.Sunt 15×3=45 bomboane si 1×3=3 prajituri. Cu bine.
diferenta a doua nr este 12 iar suma lor este 30.care sunt cele doua nr
Draga Laurenta,
Problema se rezolva in multe moduri! Ce clasa esti? De acum sa spui ce clasa esti!
Clasa a IVa:
/––––/ nr mai mare cu 12
/––/ nr mai mic(diferenta ne arata cu cat este mai mare un nr). Scadem 12 din suma si raman doua parti egale 30-12 apoi ce ne da impartim la 2 samd.
Clasa a VIIIa:
x-y=12 si x+y=30 se rezolva sistemul format cu ele.
bună seara, sunt Denis va rog dacă mă puteți ajuta la urmatorul exercitțiu, dar vă rog dacă se poate cu explicații pentru că vreau tare mult să le înțeleg, din păcate la școală nu am reușit să le înțeleg. Mulțumesc mult.
este cu fracții și 1/2 este 1supra 2
S=1+1/2+1/2^2+…..1/2^2014
Draga Denis,
Iata la ce m am gandit eu! Inmultim cu 2 suma data si obtinem 2S=2.1+2.1/2+2.1/2^2+…2.1/2^2014 sau(1) 2S=2+1+1/2+…1/2^2013(dupa inmultire si simplificare).Din rel 1 scadem suma data si obtinem 2S-S=2+1+1/2+1/2^2+…1/2^2013-1-1/2-1/2^2-…-1/2^2014. Observam ca se reduc doi cate doi, si ne ramane S=2-1/2^2014 sau S=2(1-1/2^2013).Cu bine!
Buna ziua !
Va rog sa ma ajutati la aceasta problema :
– In sfera f ( O, 4√3 dm) e inscris un con circular drept a carui sectiune axiala este un triunghi echilateral. Aflati generatoarea.
Draga Antonia,
Faci o sectiune prin sfera si sectiunea axiala conului si obtii un triunghi echilateral inscris intr un cerc mare al sferei! E greu de desenat aici!Cu bine.
ce numar inpartit la 26 sa ne deie 88
Draga Maria,
a:26=88 de unde a=88×26. Te las pe tine sa faci inmultirea! Cu bine.
Buna ziua,
puteti sa ma ajutati la rezolvarea problemei de cl. 5
Luca are de 4 ori mai multi bani decat Andrei, Matei are de 3 ori mai putin bani decat Luca. Imreuna au 76 lei. Cati bani are Andrei.
/==/==/==/==/==/==/==/==/==/==/==/==/ Luca
/==/==/==/==/ Matei
/==/==/==/ Andrei. Am ales pentru Luca 12 parti pentru ca se imparte si la 4 si la 3. In total 19 parti. 76:19= o parte. Apoi af;i cat are fiecare. Cu bine.
Buna ma puteti ajuta cu aceasta problema;
Bunicul are mai mult de 50 de ani ,dar mai putin de 70.Fiecare din fi are atatia copii ca numar de
frati .Numarul total de fi si de nepoti este egal cu varsta bunicului.Cati nepoti si cati fi are bunicul?
Draga Giulia,
Nu mi ai spus ce clasa esti!Iata o rezolvare, care nu stiu daca ti va folosi! Bunicul are x fii; fiecare are x copii; in total vor fi x.x copii. Suma fiilor bunicului cu numarul copiilor lor, varsta bunicului, deci 50
Buna ziua, ma puteti ajuta si pe mine?… Daca a-[√3]+[0,16]={√3}+{1/2}+{4,3}, sa se determine [a] , {a}, [5a]
Draga Stefania,
Nu mi ai spus ce clasa esti! Ceea ce mi ceri tu, se face la cercul de matematica! Poti sa te informezi pe internet si sa rezolvi exercitiul!Cauti partea intreaga si partea zecimală a unui număr real. Cu bine!
Vă rog,dati-mi un sfat cu sa abordez problemele de cls 5,în special cele care se rezolva prin metoda figurativa!Mulțumesc!
Razvan,cls 5
Draga Razvan,
Aici pe site ul nostru gasesti multe probleme explicate si rezolvate prin metoda ficurativa! E bine sa le rezolvi si tu, sa le intelegi! Cu cat vei face mai multe si mai variate va fi in avantajul tau! Cu bine!
buna seara va rog sa ma ajutati la acest exercitiu 7.Efectueaza a)6×4+9×5-12:6
Efectuează întâi înmulțirile și împărțirile, în ordine, apoi adunările si scaderile.
Scuze de deranj. O problema de clasa a 3 a.catul a 2 numere este 7, iar diferența lor 30.aflați numerele
Draga Alina,
Daca avem catul 7, inseamna ca un numar este de 7 ori mai mare decat celalalt!
/…/…/…/…/…/…/…/ numarul mai mare
/…/ numarul mai mic. Diferenta are 6 parti si este 30.O parte va fi 30:6=5. O parte este 5. Numarul mai mare este 7*5=35, iar cel mai mic este 5. Cu bine.
corect
Diferența a două numere este 40 . sfertul primului număr este cu 5mai mare decât o treime din al doilea număr . Care sunt numere?
Rezolvare prin metoda figurativa…
Eventual poți adăuga, dacă tot ai pretenția să îți rezolvăm tema, un „te rog”! Știi, aici nu răspund roboți, ci oameni, care fac voluntariat…! Dar politețea a dispărut!
|__________________|
|_______________|__|
|__________________|__________________|__________________|__________________|
|_______________|_______________|_______________|..........40...............|
Desenăm cele 4 sferturi ca fiind treimea + 5
|_______________|__|_______________|__|_______________|__|_______________|__|
|_______________|_______________|_______________|..........40...............|
Și de aici un copil isteț observă că avem de 4 ori segmentul de 5, 5 x 4 = 20; 40- 20 = 20. Îl scădem din ambele numere.
|_______________|_______________|_______________|_______________||_______________|_______________|_______________|..........20...|
Și de aici se observă că o treime este egală cu 20… așadar numărul mai mic este 3 x 20 = 60, iar numărul mai mare (20 + 5)x 4= 100
Când facem proba, 100-60 = 40 – ceea ce știm din problemă
Cu plăcere!
Bună seara mă numesc Nicoleta! Sunt în clasa a IV-a și aș dori să mă ajutati cu o problemă!
Trei copii colectioneaza timbre.Ei au clasoare identice.La un moment dat primul copil observa ca ii mai sunt necesare 14 timbre ca sa completeze clasorul, al doilea copil observa ca ii mai trbuie 16 timbre sa completeze clasorul, iar al treilea copil constată ca ii mai sunt necesare 18 timbre pentru a-si completa clasorul. Al treilea copil mai observă ca, dacă ar da toate timbrele pe care le are celorlalti 2,aceștia ar avea clasoarele complete.
Cate timbre sunt intr-un clasor?
Eu m.am gandit sa fac asa segmentele: |____|+14
|____|+16
|____|+18
Dar nu stiu daca e bine si daca da nu am idee cum sa fac
1. De câte timbre mai au nevoie C1 și C2? (copil 1 și copil 2)
14 + 16 = 30 (timbre)
* înseamnă că al treilea copil are 30 timbre, dacă le dă celorlalți și au clasoarele complete.
2. Câte timbre are clasorul lui C3?
30 + 18 = 48 (timbre)
* dacă clasoarele sunt identice, fiecare are 48 de timbre. Aici nu îmi este clară întrebarea. Se referă la câte timbre poți pune într-un clasor? Am aflat deja. Dacă se referă la câte timbre are fiecare copil în clasor, atunci continuăm.
3. Câte timbre are C1?
48 – 14 = 34 (timbre)
4. Câte timbre are C2?
48 – 16 = 32 (timbre)
* mai poți afla și câte timbre au împreună cei trei copii.
Cred că metoda figurativă nu e cea indicată… dar ar arăta așa:
–––––––––––––––––- – copilul 3, cu albastru ai 14 t pe care i le da lui c1, cu rosu 16 t pe care i le da lui c2, si cu verde 18 care sunt ale lui.
––––––––––––-––––– – copilul 1, cu portocaliu ce avea el, cu albastru ce a primit, totalul – 48, stim de la primul copil.
–––––––––––-–––––– – copilul 3, cu rozce avea el, cu rosu ce a primit, totalul – 48, stim de la primul copil.
Nu pornești cu segmente egale! Ei au „egal” doar segmentul final, pentru că sunt identice clasoarele.
Pingback: Probleme care se rezolvă prin metoda figurativă (II) | Talente de Năzdrăvani
Buna ziua!se poate va rog sa ma ajutati sa rezolv urmatoarea problema de clasa a VI a?banuiesc ca se poate rezolva si prin metoda figurativa, dar mai mult de atat, nu realizez cum se poate face. Ma puteti ajuta,va rog?
Liliana,Roxana si Elena au fost la cumparaturi cu un total de 261 de lei. Fiecare dintre ele avea o suma diferita de bani. Liliana a cheltuit 2/3din banii ei, Roxana a cheltuit 1/2 din banii ei, iar Elena a cheltuit 3/4din banii ei. Fiecare a cheltuit aceeasi suma de bani. Cati bani a avut fiecare la inceput?
Pingback: Metoda grafica/figurativa - Blog de oameni mari cu copii mici
Buna seara. Sunt in clasa a V-a. Va rog sa mă ajutați la o problema.
In parc au înflorit cu 172 bujori mai mulți decât zambilelor. Știind că numărul bujorilor este de 3 ori mai mare decât numărul zambilelor, afla cate flori sunt din fiecare fel.
Draga darius,
/––-/ numarul zambilelor
/––-/––-/––-/numarul bujorilor.Diferenta are doua parti, adica 172, O parte 172:2=86. Deci sunt 86 de zambile si 86×3=258 bujori. Cu bine.
Deleanu Darius. Buna seara, sunt in clasa a v-a , va rog sa mă ajutați la o problema cu metoda figurativă.
In parc au înflorit cu 172 bujori mai mulți decât zambile. Știind că numărul bujorilor este de 3 ori mai mare decât numărul zambilelor, afla cate flori sunt din fiecare fel.
Va mulțumesc !!!
Buna ziua,sunt Darius,elev in clasa a IV-a si va rog sa ma ajutati cu urmatoarea problema
Tatal, mama, si cei trei copii ai lor, au impreuna 82 de ani. Varstele fiilor sunt reprezentate prin numere naturale consecutive pare. Aflati varsta fiecarui membru al familiei, stiind ca la nasterea celui de-al doilea copil, fiecare din parintii lui avea de treisprezece ori varsta primului copil. Va multumesc!
Draga Darius,
Iata parerea mea.Cand se naste al doilea copil, primul avea 2 ani. Parintii aveau 13*2=26 de ani. Cand se naste al treilea copil, parintii au 26+2=28 de ani(copii au varste numere pare consecutive).Anii care trec din acest moment, se adauga tuturor.Notam cu un segment acesti ani!
/––/+28 tata
/––/+28 mama
/––/ al treilea copil
/––/+2 al doilea copil
/––/+4 primul copil. Scadem din 82 suma 28+28+2+4=62. adica 82-62=20. Acesti 20 ani trebuie impartiti in 5 parti egale( cele 5 segmente). 20:5=4ani. Deci, tata si mama au cate 28+4=32 ani, primul copil 4+4=8 ani, al doilea 4+2 =6 ani, al treilea 4 ani.Verificare 32+32+8+6+4=82. Cu bine.
Va multumesc mult!
Cu placere! Te mai asteptam!
Doina elevi au aceeași suma de bani.Primul cheltuiește într o excursie 1000 lei iar al doilea 200 lei. Stiind ca primuluite elev îi rămâne o suma de doua ori mai mare decat a celuilalt elev,aflați ce suma au avut initial
Cred că problema nu e corectă. Dacă au aceeași sumă inițială, nu este posibil ca cel care cheltuie 1000 lei să rămână cu o sumă mai mare decât cel care cheltuie 200.
Verificați datele.
Mă ajutați și pe mine? Sunt Diana Sima, de clasa a IV-a si am o problemă destul de ciudată: Ana ii spune Mariei: dă-mi 17lei și voi avea o suma de 4 ori mai mare decât a ta. Maria îi răspunde: mai bine dă-mi tu 13 lei si vom avea amândouă sume egale. Câți bani are Ana? Dar Maria?
Mi se pare imposibilă! Multumesc!
Nu este imposibilă, doar necesită multă experiență în rezolvarea de probleme!
Să le luăm pe rând: Maria îi răspunde: mai bine dă-mi tu 13 lei si vom avea amândouă sume egale.
De aici înțelegem astfel: Ana are mai mulți bani decât Maria. Diferența pe care o are în plus, dacă o împarte în jumătate și îi dă Mariei, amândouă vor avea sume egale. Dar știm că Maria primește 13 lei ca să aibă în mod egal. Așadar jumătatea diferenței este 13. Concluzia: Ana are cu 26 de lei mai mult decât Maria.
|_________| (Maria)
|_________|_________26___| (Ana)
Mai departe: (aici va fi destul de greu sa fac desenul pe calculator, sper sa intelegi)
Ana ii spune Mariei: dă-mi 17lei și voi avea o suma de 4 ori mai mare decât a ta.
Asadar, daca luam 17 lei din suma Mariei si o adăugăm Anei, Ana va avea de patru ori mai mult decât ceea ce îi rămâne Mariei. Pe lângă cei 26 de lei diferentă între ele, acum se mai adaugă și 2 x 17 lei. Însă știm că are „de 4 ori mai mult”, așadar diferența dintre ele, reprezentând 3 părți egale, este acum de 26+2×17.
|______|.17.|
|______|_17___|______|____17_|
26+17+17=60 (diferența de bani dintre cele două fete, dacă Maria i-ar da Anei 17 lei din suma ei)
3 părți egale reprezintă 60
60: 3=20 (suma de bani a Mariei, după ce i-a dat Anei 17 lei)
20+17=37 (suma de bani inițială a Mariei)
37+26=63 (suma de bani inițială a Anei)
R: 37; 63.
Verificare:
37+13 = 63-13 (verificăm dacă este adevărat pentru Maria îi răspunde: mai bine dă-mi tu 13 lei si vom avea amândouă sume egale.)
50 = 50 (adevărat) – soluțiile sunt corecte.
Buna seara. Sunt in clasa a 4-a si va rog frumos sa ma ajutati si pe mine. Nu inteleg cum sa transpun o problema in metoda grafica, cu segmente.
Intr-un parc sunt 18 fete si baieti. Daca ar pleca 7 fete ar ramane cu 3 baieti mai multi decat fete. Cate fete si cati baieti au fost initial?
Am rezolvat-o dar nu stiu sa o reprezint grafic
18-7=11 copii
11-3=8
8:2-4
4+3=7 baieti
4+7= 11 fete
Va multumesc si va doresc o seara frumoasa.
Imi puteti recomanda o carte de matematica cu metoda grafica explicata bine ?
Nu există „metoda grafică explicată bine”, există prima explicație, așa cum ai și aici în articol, și foarte multe probleme de rezolvat. După ce rezolvi singură măcar vreo 50, de diverse tipuri, vei vedea că metoda nu mai e atât de dificilă. Poți folosi și cele aproape 3000 de comentarii la acest articol pentru a desluși tainele metodei.
Pentru problema ta,
|___________________|_____7_____| (fete)
|___________________|__3__| (baieti)
Problema se rezolvă:
18 – (7+3) = 8
1+1=2 (părți egale)
8: 2 = 4 (o parte egală, adică numărul de fete rămase după ce au plecat 7)
4+7 = 11 (fete)
18-11 = (7 băieți)
sau:
4+3=7 (băieți)
R: 11; 7
Verificare: 11+7=18 (A)
Buna ziua ! Va multumesc pentru raspuns si pentru sfat. O zi buna si LA MULTI ANI !
Multumesc!
Si… spor la lucru!
Buna ziua. Ma numesc daniela si dun5 in clasa a a 4a.am o problema pe care no o inteleg.
Daca fete si baietii care participă la un joc ar forma echipe fata-baiat, 8fete ar rămâne in afara jocului. Daca insa ar forma echipe compuse din 3fete si un baiat,atunci doi baieti raman in afara jocului. Afla cate fete si cati băieți sunt.
Este o problemă mai dificilă, tot cu metoda figurativă.
f-b f-b …. f-b f f f f f f f f
De aici știm că sunt cu 8 mai multe fete decât băieți
Problema ne spune că se rearanjează și formează alte echipe:
f-f-f-b f-f-f-b … f-f-f-b b b
De aici începe cheia problemei…
Câte fete au fost redistribuite pentru a forma noile echipe?
2 – din echipele băieților rămași singuri (inițial aveau și ei repartizată câte o fată)
și încă 8 – fetele care la început nu erau în nicio echipă.
În total, 10 fete redistribuite.
Câte fete s-au redistribuit în fiecare echipă?
Era una, sunt 3, așadar 3-1=2 fete redistribuite într-o echipă
10:2=5 (echipe nou formate cu câte 3 fete)
Câți băieți sunt?
5 + 2 = 7 (5 sunt în echipele noi și 2 fără echipă)
Câte fete sunt?
3 x5 = 15 (dacă înmulțim numărul de echipe cu 3, câte sunt într-o echipă)
sau
7 + 8 = 15 (numărul de băieți plus cele 8 fete singure din prima așezare)
Sper că îți e de ajutor.
Buna. Problema pt cls a 3a
Paul are de 7 ori mai multi bani decat sora lui, miruna. Cati lei are fiecare, stiimd ca Daca Paul ii fa Mirunei 450 lei, atunci cei doi frati ar avea sume egale.
Paul are de 7 ori mai mulți lei decat sora lui, Miruna.
Câți lei are fiecare, stiind ca, daca Paul îi dă Mirunei 450 lei, atunci cei doi frați ar avea sume egale.
Scuze, am transcris problema, nu mă puteam concentra la matematică din cauza scrierii deficitare.
Dacă Paul îi dă Mirunei, atunci Paul are mai mult decât Miruna. El îi dă surorii jumătate din ce are el în plus față de ea, ca să egaleze sumele. Dacă știm că îi dă 450 lei, înseamnă că diferența dintre ei este de 900 lei.
De asemenea, știm că el are de 7 ori mai mult decât sora sa. Observăm din desen că celor 900 de lei le corespund 6 părți egale.
Calculăm cât reprezintă o parte egală: 900: 6 = 150 (lei o parte egală, adică suma Mirunei)
Pentru a calcula suma lui Paul, 150 x 7 = 1050 lei sau 150 + 900 = 1050 lei.
|_______|
|_______|_______|_______|_______|_______|_______|_______|
Sper că ai reușit să înțelegi.
Pingback: Probleme Care Se Rezolva Prin Metoda Figurativa Clasa 4 Proiect Didactic - elicad.space
Bună ziua ! Sunt în clasa a V a și nu dau de cap unei probleme…Într-o excursie, un elev cheltuie în prima zi cu 30 lei mai puțin decât o treime din suma pe care o are. a doua zi cheltuiește o treime din suma rămasă. a treia zi cheltuieste jumătate din banii ramasi, iar a patra zi cheltuieste ultimii 80 de lei. Am ajuns la niște sume, dar când verific, nu ies. .
De exemplu, dacă a 4 a zi cheltuiește 80, înseamnă că a 3 a zi avea 160 lei… Dar nu e corect dacă în a 2 a zi îmi dă 480… Mă ajutați să o înțeleg?
Problema este la metoda mersului invers, cu reprezentare grafică.
|______________________|______________________|______________________| – suma lui, împărțită în trei
|_______________|______| – primul segment = cât chetuie în prima zi, fără al doilea, care reprezintă 30 lei.
|_______________|______|______________________|______________________| – suma cu care rămâne, și pe care, la rândul ei, o împarți în trei
|_______________|________________|___________________|_______________|
|_______________|________________| – cât cheltuie a doua zi
|_______________|________________|___________________|_______________| – cât îi rămâne după a doua zi
|_______________|________________|___________________| – cât cheltuie a treia zi
|_______________|________________|___________________|_______________| cei 80 lei rămași
80*2 = 160 lei rămași după a doua zi
80*3 = 240 lei rămași după prima zi
240-30 = 210 lei – 2/3 din suma inițială
210:2×3= 105×3=315 lei a avut la început
Graficul îl vei vizualiza corect pe un ecran mare, landscape, nu pe telefon!