Lecția despre piramidă

Am ajuns la capitolul meu preferat din manualul de matematică: elemente de geometrie. Aici mă simt ca peștele în apă și afirmații din categoria „dar dumneavoastră chiar vă place“ nu mă fac decât să mă simt foarte bine. Se adaugă și satisfacția muncii de cinci ani, ale cărei roade încep să fie bune de cules.

Înainte de a începe să desenăm, am readus în prim plan imaginea piramidelor egiptene. Ne-am raportat întâi la pătrat, care ne iese ușor desenat pe pătrățele. Cu mici artificii și alunecări de echer, iese și pe foaie velină. Dar cum oare au marcat acum mii de ani pătrate perfecte în deșert, cu laturile de sute de metri? Clar, extratereștri, omul nu e capabil de așa ceva! Însă până elucidăm misterul piramidelor, am încercat să ne dumirim ce e cu aceste corpuri speciale.

Am stabilit că baza trebuie să fie un poligon și că pot construi o piramidă pornind de la orice formă. Dacă o vor „frumoasă“, ca a egiptenilor, atunci trebuie să aibă un pătrat la bază și să aibă vârful fix deasupra intersecției diagonalelor. Dar nu doar acestea sunt piramide. Nu aș vrea să rămână cu această idee.

Așadar, era nevoie de soluții.

Câteva zile m-am tot gândit că cele două modele din setul meu cu corpuri, una patrulateră, una triunghiulară, ambele regulate, nu îmi dau acea variație care există în lumea din jurul nostru. M-am gândit apoi să confecționez eu unele și eram convinsă că am acasă bețișoare de lemn să rezolv problema. Așa m-am trezit cu o zi înainte, prea târziu, că n-am piramidele pe care le voiam, din lipsă de material didactic în bucătărie.

Însă un obstacol nu e decât o nouă provocare de a găsi altă soluție. Am inventariat în minte dulapul de la școală. Ață suficient de groasă cât să se vadă și din spatele clasei… nu aveam. Dar aveam câțiva metri buni de elastic!

Și atunci s-a aprins beculețul: am copiii care pot fixa vârfurile, iar baza o pot improviza. În plus, faptul că puteam avea un vârf mobil nu urma decât să ușureze generarea unor situații diferite care să se încadreze în familia piramidelor.

O bancă a fost perfectă pentru ridicat o piramidă patrulateră, ca apoi s-o bată „vântul dorinței“ în toate părțile. Și ca să avem și una triunghiulară, am folosit același procedeu, dar cu un echer pentru tablă. Pentru fiecare piramidă, am schimbat copiii, ca să o vadă cum „se ridică“ din mâinile lor. Muchiile elastice s-au comportat extraordinar.

Pozele de mai sus sunt realizate, cu ajutorul lor, în pauză. Dar de ce le puneți pe instagram? Pentru că e păcat ca o idee bună să se piardă, poate vor să o folosească și alții!

Spre final…

Bineînțeles că și lor le vin idei. În timp ce desenau – au vrut să încerce cu pentagon și hexagon la bază – aud un Ahhhh, sigur o să avem temă să construim!.

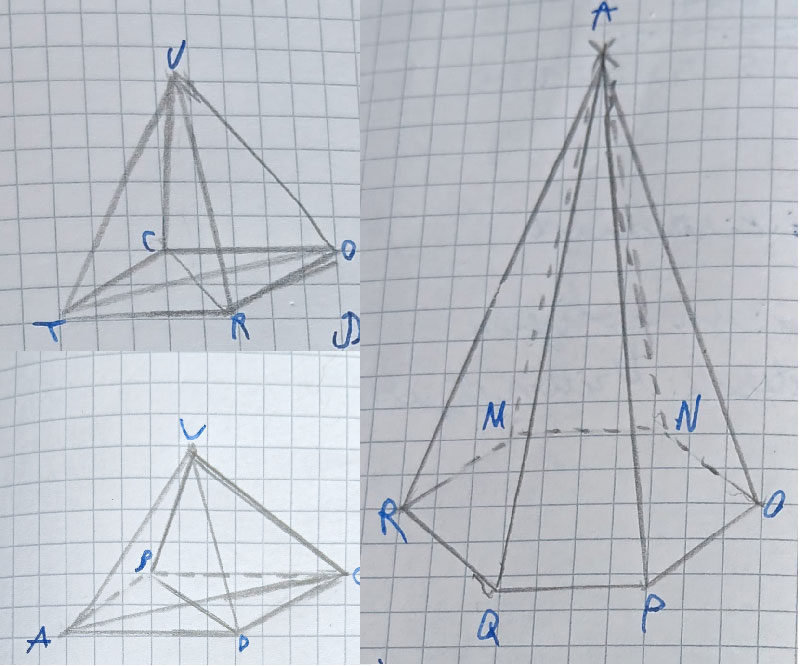
Credit foto: Matei M.

Credit foto: Eric M.

Și da. Au avut, căci manualul este extrem de „subțire“ la capitolul „sarcini de lucru“. Însă au deprins repede utilizarea compasului și nu le-a dat mari bătăi de cap.

View this post on Instagram

A post shared by Talente de Năzdrăvani (@talente_de_nazdravani)

Matematică distractivă: campionat de tabla înmulțirii

Toamna aceasta m-am distrat nemaipomenit, căci parcă s-au potrivit toate în categoria „oamenii își fac planuri și Dumnezeu râde în hohote“. Așadar le-am luat și eu pe toate cum au venit, m-am descurcat cu ele cât de bine am putut, am schimbat listele de priorități și până acum sunt pe linia de plutire. N-am prea avut timp de scris, deși se strâng destule de povestit, dar pentru cele ce urmează am rupt o bucățică de timp. Aici pe blog e „picătura“ mea de liniște și relaxare, nu puteam să ratez.

După vacanța de noiembrie școala noastră (ca de altfel foarte multe altele) a ales să fixeze școala altfel. Atât de în scurt au fost toate, că pe la niciun muzeu mare n-am mai găsit locuri cu programare (însă tot răul spre bine, nu aș fi ajuns la un altul care m-a surprins foarte plăcut!). Să găsești însă activități gratuite, dar și interesante, nu e însă o provocare simplă. De bine, de rău, programul s-a schițat până la urmă și vineri, după activitățile sportive, am rezervat două ore de „matematică distractivă“.

Copiii au oftat!

Anul trecut am avut concurs, probleme ascunse sub coduri QR, cu puncte ce puteau fi câștigate. Cum suntem deja în al cincilea an împreună și ne cunoaștem reciproc, pe la începutul săptămânii m-au întrebat pentru cine va fi distractivă matematica? Pentru ei sau pentru mine, pe seama lor? N-am zis nimic, mai ales că nu mă hotăram încă ce anume să fac. Jocuri, enigme, parcă toate păreau, cum ziceau și ei, distractive pentru mine.

Și ideea câștigătoare a venit tot de la copii. La after, cum era școala altfel și nimeni nu avea teme, am zis să utilizăm constructiv timpul disponibil și să exersăm tabla înmulțirii, pentru că noul capitol bate la ușă și nu va fi ușor. Le-am cerut să își instaleze o aplicație în acest sens, dar, cum sunt multe disponibile, printre cele pe care le-au încercat exista și varianta „duel“. M-am simțit ca Arhimede, dar n-am strigat și „evrika“. Joi i-am anunțat să ia tabletele a doua zi, iar dacă au timp, să exerseze tabla înmulțirii.

View this post on Instagram

A post shared by Talente de Năzdrăvani (@talente_de_nazdravani)

Buuun, după ce am instalat toți aceeași versiune de aplicație (mie mi-a plăcut că exersai nu numai tabla înmulțirii, ci și aflarea factorului necunoscut), am desenat pe tablă schema ca la campionate. Zâmbeam și-mi aduceam aminte cum completam cu tata, pe schema decupată din ziare, țările la campionatele mondiale de fotbal. Cam așa și acum, urma să stabilim un câștigător. Băieții au recunoscut imediat organizatorul grafic, iar pe măsură ce se desfășurau meciurile, auzeam: Eu am pierdut în sferturi . sau Cine joacă finala mică?.

Doamna, și ce primim??

Cred că a fost prima întrebare. Un premiu surpriză, normal, pe care nu l-am divulgat ca să nu se emoționeze prea tare. Însă au avut grijă să negocieze ca și cel de-al doilea jucător al „finalei“ să aibă parte de un premiu de consolare, chiar înainte să afle despre ce este vorba…

În centru se desfășura jocul principal, dar pe margine fiecare făcea pereche cu un coleg și se „antrenau“. Sau se jucau pur și simplu să vadă cine e mai rapid, cine știe mai bine, cine se descurcă la înălțime. Cert e că am avut aproape două ore de exersat intens, dar și de emoții și strategii. Să vedeți palpitații la tragerea la sorți, când, pe măsură ce se completau locurile pe tabel, își dădeau seama dacă au un parcurs mai ușor sau mai greu spre finală, dacă riscă să întâlnească un adversar redutabil sau nu.

Sau când au realizat că, având un absent, una din partide se câștiga automat, la masa verde. Și pentru a ști cine este „norocosul“, trebuia să ai răbdare până se scria pe tablă ultimul nume, pentru că nimeni nu știa ce număr este scris pe biletul rămas pe masă.

La a doua tură de joc, eliminarea primului câștigător a fost salutată fără fair-play, iar când i-am atenționat, au protestat, că ei nu se bucurau de eliminare, ci că au și ei o șansă mai mare la câștig. Au avut parte și de surprize, colegi cărora nu le dădeau șanse, dar care i-au băgat repede în corzi. Oricum, m-am distrat și eu, dar și ei.

campionat_tabla_inmultirii

Acordarea premiului a fost ca-n vulpea și strugurii.

Când timpul se apropia de final și am aflat și al doilea învingător, i-am anunțat că premiul este un Fb la matematică. Și premiul de consolare? Ei bine, la următorul test, locul al doilea are un nivel bonus la calificativ. Dar… am avut și voci care au spus că premiul nu e mare scofală, că, până la urmă, oricând te poți strădui să iei un Fb la matematică, deci ce atâta bucurie pentru nimic!

Ba puteam și eu să vin cu un premiu mai interesant, nu așa… ceva mărunt pentru care nici nu merita să participi, darămite să te chinui să și câștigi. Câștigătorii n-au fost de acord, chiar dacă nu de Fb-uri duceau lipsă, s-au bucurat de victorie din tot sufletul.

Eu… m-am bucurat de bucuria lor și pentru că am reușit, măcar pentru o perioadă, să îi fac să uite că, de fapt, exersează la matematică.

Axa de simetrie

Capitolul meu preferat din manualul de matematică, începând cu clasa a doua, apoi a treia, și mai ales la clasa a patra, este cel dedicat elementelor de geometrie. Avem timp acum, în clasele primare, să punem bazele necesare unor deprinderi corecte de lucru cu instrumentele de geometrie. Timp pe care, să recunoaștem, profesorii nu îl au la gimnaziu. Ori poate nu vor să îl aibă.

Mă declar aproape mulțumită de modul în care copiii mei trag linii pe pătrățele. Rigla parcă nu se mai mișcă din loc, cu mici excepții avem linii strâmbe sau deviate de la traseu. Pentru mine e o dovadă că a cere riglă mică în penar de la clasa pregătitoare și a o folosi cu orice ocazie (a se citi orice tabel, de câte ori e nevoie, se desenează cu rigla) a fost o decizie înțeleaptă, oricâte dureri de cap mi-a dat. Normal că e loc și de mai bine, dar paharul nu e mai mult gol decât plin.

O lecție la care joaca și imaginația anticipativă se îmbină în cel mai plăcut mod este lecția dedicată axei de simetrie.

Aș fi susținut acum ceva vreme că nu există copil care să nu poată înțelege acest concept geometric. Vorbesc despre orice copil care nu are niciun fel de dificultăți. Până m-am convins singură. Copilăria a fost petrecută cu ochii în ecran sau la diverse sporturi, a declarat că el niciodată, dar niciodată, nu a făcut proiecte artistice, la grădiniță nu a mers și la școală „nu aveau timp“.

A ajuns la mine în clasa a patra. Am încercat orice, de la fluture pictat pe jumătate și imprimat în oglindă, la origami și desene, figuri îndoite. Părea că e ok, dar când trebuia să ilustreze singur, desenând pe pătrățele ceva simetric față de o dreaptă dată, pur și simplu… se bloca. Exerciții pe care la școală, cu clasa a doua, le făceam cu viteza luminii, la el nu ajungeau la niciun rezultat. Nu am reușit să îl ajut.

Simetria în joacă – figurine decupate. Detalii aici.

Lecția la clasă

Am povestit deja acum doi ani, în mare parte, cam cum desfășor lecția, găsiți aici pe blog articolul. Anul acesta însă, pentru că știu că pot face ceea ce le cer, am decis să îi implic în pregătirea materialelor ce trebuie decupate.

Cu vreo două zile înainte de desfășurarea activității, le voi da două pagini imprimate să-și decupeze singuri figuri geometrice ale căror axe de simetrie le vom căuta. Așadar vor avea pe listă cerc, cele trei tipuri de triunghiuri (oarecare, isoscel, echilateral), pătrat și dreptunghi, paralelogram și romb, dar și mult-iubitul hexagon regulat.

Chiar dacă la clasa a treia nu învățăm toate aceste figuri, nimic nu ne împiedică să ne familiarizăm cu forma. Ei întreabă cum se numesc, eu le spun, dacă rețin, nu le dăunează sănătății. Le vom folosi și în clasa a patra unde, cu excepția hexagonului, toate sunt pe listă.

Figurile sunt suficient de mari pentru a putea fi manevrate, iar fișierul printabil este disponibil aici timp de o săptămână de la publicarea articolului. După această dată, este disponibil la cerere persoanelor care susțin printr-o donație acest site.

Surprizele perimetrului

Experiența ultimilor ani, atât la școală, cât și în privat, cu noțiunile despre perimetru îmi dădea o stare de acută neliniște pe măsură ce se apropia și la această serie momentul zero. Și, deși iubesc geometria și am făcut tot ce am putut în trei ani și jumătate cu ei ca să pregătesc terenul pentru încercările de foc ale ultimelor două clase primare, tot aveam emoții.

View this post on Instagram

A post shared by Talente de Năzdrăvani (@talente_de_nazdravani)

Undeva prin iarnă, când am aflat că în martie mai am de susținut o inspecție, făceam haz de necaz cu colega mea: să vezi de n-o să pic eu la perimetru! De multe ori în viață am zis că nu mai cobesc. Aflu data, număr pe planificare… ce să vezi, a doua lecție la perimetru. Puteam să jonglez să schimb. Dar uneori e bine să le iei așa cum au fost „scrise“.

Prima lecție și prima surpriză

Ziua de dinainte. Începem, ca de obicei: dacă au mai auzit cuvântul, dar nu la matematică. Sigur. La jocuri, perimetrul înseamnă incintă, zonă delimitată. Bun. Limite. Margine. Avem de ce să ne legăm.

Materialul didactic pentru prima lecție era foarte – cum să zic – simplu. O panglică de vreo 2m din hârtie creponată și o bancă. Nu știu de ce, nimeni nu agreează banca aceea, e cu 10 cm mai joasă decât celelalte, dar este mai mare ca suprafață. Însă nimeni nu o vrea. Și cum este în plus în clasă, necesară doar celor de după-amiază, toți o dau la o parte dacă o găsesc cumva în rând.

Așadar, le-am spus că îmi doresc să înfrumusețez această bancă, lipindu-i o minunată panglică colorată pe margine, poate o să le placă și o vor folosi. I-a umflat râsul. Băieții au comentat că, dacă panglica nu ar fi verde, ci roz, poate vor fetele. Revenim la întrebarea de bază: am pregătit eu suficientă panglică pentru a pune în practică ideea?

Și tocmai când se ridicase jumătate din numărul posibil de mânuțe, intră colega mea cu o problemă urgentă. Rezolvați voi, revin în două minute. Din spatele clasei, unde încercam să scurtez dialogul, văd cum roiul de entuziaști dă năvală cu riglele de 15cm din trusa de geometrie să „rezolve“ problema. Tocmai mă pregăteam să intervin când aud ceva ce îmi spune să mai am răbdare.

Dar de ce vă chinuiți, hai să luăm rigla mare! Adică rigla de 1m din trusa mea de geometrie pentru tablă. Așadar, din toată grămada, unul singur a venit cu ideea genială și restul s-au conformat imediat. Doar am supravegheat apoi cum e măsurată și panglica, și dimensiunile băncii.

Dar nu e tot. Era abia prima surpriză.

Au măsurat, au notat și mi-au dat răspunsul. Panglica nu ajunge, mai aveam nevoie de o bucată de 60cm, căci are 180 și am nevoie de 240. Wow. Aplauze, laude, toată lumea la loc în bănci, hai să ne liniștim și să vedem ce-am aflat.

Desenez repede un dreptunghi, notez și eu ce-au măsurat ei și „mor de curiozitate“ să aflu cum au calculat. Și aici trebuia să-mi iau un scaun, căci nici în cele mai frumoase vise ale mele nu credeam că o să văd toate variantele de calcul pentru perimetrul unui dreptunghi.

Prima, clasic, le aduni pe toate, scrisă în două variante, L+L+l+l și L+l+L+l. Doamna, dar e mai ușor cu înmulțire, 50×2+70×2! Și a venit și a treia… Eu am făcut altfel… 50+70 și am înmulțit cu 2. Uite-așa momentul meu de introducere a devenit o bucățică rezolvată din lecție. Restul a curs de la sine. Aproape că mi-au dictat ei.

Și morala…

M-am apucat să îl laud pe cel care a avut ideea să caute un instrument mai potrivit pentru a măsura banca. Modest copilul, a spus că lui i s-a părut „logic“. Am râs un pic, căci am scuturat de praf o expresie pe care ei au tot căutat să o explice, instinctul de turmă, cum s-au dus buluc și se chinuiau să măsoare.

Și acum a venit lovitura de grație. Doamna,dar și eu am vrut să iau rigla mare. // Și de ce nu ai luat-o? // Păi… dacă toți făceau cu cea mică… nu am vrut să fiu eu singurul care face altfel!

Așadar, cam aici ne situăm la 9 ani. Știi că nu e bine, sau mai bine zis nu e greșit, ai o idee mai bună, știi că ai o idee mai bună, și totuși nu îți asumi să ieși în față, să fii altfel decât ceilalți. Tot optimismul meu cu reușita perimetrului s-a înecat. Degeaba suntem super-isteți dacă nu avem curaj să fim diferiți și să schimbăm lucrurile în jurul nostru.

Epilog

Perimetrul a continuat cu „miracolul lui Pitagora“. I-am pus să deseneze pe pătrățele un triunghi care să aibă laturile de 3 și 4 cm. Pe pătrățele iese mereu unghi drept. Dacă desenați corect, a treia latură are 5 cm, apoi calculați perimetrul. Normal că le-a ieșit. Doamna, ați avut dreptate!! De unde știați?? — Nu am știut eu. Acum 2500 de ani a aflat-o un grec pe nume Pitagora. (De când am făcut poligoane din elastic întins de ei și le-am denumit, au devenit mari fani ai grecilor pentru limba lor.)

A doua lecție a curs apoi lin, așteptăm provocările de la concursuri, minunatele probleme rezolvabile prin metoda figurativă ce implică perimetrul, garduri, rânduri de sârmă și multe, multe altele.

Bunicul are o livadă pe un teren de formă dreptunghiulară, cu lungimea de 60 m și lățimea de 40 m. Vrea să îl împrejmuiască cu un gard, lăsând spațiu pentru o poartă lată de 5m. Câtă sârmă este necesară pentru a realiza gardul, dacă între stâlpi sunt două rânduri de sârmă?

Lecțiile de geometrie, între pasiune și știință

Contează cu ce te joci la vârsta grădiniței? Normal… Contează enorm ce atingi, ce așezi, ce observi, toate pentru a forma în mintea copilului o imagine corectă a lumii înconjurătoare. Când vine vorba de forme și corpuri geometrice, lipsa interacțiunii cu obiecte se observă imediat. Banalele jocuri de construcție din lemn sunt baza cunoștințelor de geometrie ale copiilor și lejeritatea cu care abordează geometria la gimnaziu își are originile aici, în jocurile de grădiniță și, mai apoi, în cele utilizate pentru a diferenția corpurile în clasele primare.

Eu nu sunt cel mai bun exemplu de referință, pentru că la mine în casă compasul, rigla și echerul au stat pe masă de când mă știu. Din setul meu de cuburi de construcție, conul, cilindrul, cubul, paralelipipedul și piramida au ajuns materiale didactice la școală. Însă de multe ori tata le construia din hârtie pentru a le arăta copiilor, cerându-le, la rândul lor, să construiască și ei. Ei erau la gimnaziu, eu la grădiniță.

Tata nu m-a învățat proprietățile cubului, însă eram capabilă să îl construiesc imitându-l. Am mers și cu el la ore și nu pricepeam pe atunci de ce copii mult mai mari decât mine se chinuiau de parcă aveau de rezolvat muncile lui Hercule ca să asambleze un biet corp.

Pentru că lor abia acum le arăta cineva, în timp ce mie… eu am avut altă șansă.

Prima abordare a elementelor de geometrie cu niște ani în urmă la clasele primare a fost însoțită de alcătuirea unei colecții măricele de obiecte de diferite forme, cât mai mari, care să îi ajute pe copii să observe atât asemănările, cât și diferențele dintre corpuri. Și, pentru că veni vorba de ceea ce fac părinții pentru a susține acasă învățarea, mă întreabă atunci o mămică dacă îmi poate trimite la școală un set de geometrie pe care îl are acasă. L-am ținut ceva timp la școală, până ne-am terminat lecțiile, iar anul următor am rugat-o să ni-l trimită din nou. Era exact ceea ce aveam nevoie.

Folding Geometric Shapes – EduClass

Ce forme ne dau bătăi de cap?

Programa de geometrie a claselor primare, strict referitoare la corpurile geometrice (nu la forme), include cubul, cuboidul (palelelipipedul) și sfera, identificare și denumire, la nivelul clasei pregătitoare. În clasa întâi se adaugă cilindrul și învățăm să le descriem, câte fețe au, ce formă au acestea. Clasa a doua vine cu prima provocare: se adaugă conul și începe construcția acestora după desfășurare dată. Ultimele două clase aduc nou piramida și noțiunile de volum pentru cub și paralelipiped, precum și provocări de construcție din materiale diverse.

Revenind la clasa a doua (provocarea mea din acest an), foarte multe materiale tipărite cer copiilor să identifice desfășurarea corectă a unor corpuri, însă de puține ori ai la îndemână posibilitatea de a le arăta exact cum se „asamblează“. Setul de geometrie pe care tocmai l-am prezentat mai sus rezolvă această problemă. Corpurile sunt confecționate din plastic transparent, se pot deschide (una din fețe este detașabilă la fiecare) și înăuntru este pliată, din plastic colorat, desfășurarea acestora. Copiii o pot strânge și deschide de atâtea ori de câte este necesar pentru a înțelege.

În plus, folosindu-le goale, am reușit să rezolv și cu copii mai mari (clasa a cincea) problema liinilor punctate atunci când desenam pe hârtie cubul și paralelipipedul. Țineam forma pe masă și ne uitam, când le desenam, ce muchii vedem fără nicio problemă și pe care le putem identifica privind prin una din fețele transparente. Setul – căci îmi e greu să îl numesc joc – este o investiție pe termen lung, de foarte mare ajutor pentru copii.

Ce conține?

Opt corpuri fac subiectul setului: cubul și paralelipipedul, cel din urmă cu o provocare pentru simțurile copilului, căci una din muchii este identică cu a cubului și trebuie să explorezi puțin ca să le diferențiezi, prin suprapunere. Apoi avem două corpuri cu fețe curbe, cilindrul și conul, ambele cu desfășurare simplă.

Pentru piramide avem două exemple, un tetraedru regulat (are fețele triunghiuri echilaterale) și una clasică, cu baza pătrat, ca cele egiptene. În completare sunt și două prisme – pe care nu le studiem în clasele primare, una triunghiulară și una hexagonală. Mie îmi plac, căci copiii le găsesc repede asemănare în lumea reală: un „acoperiș“ și un fagure de albine.

De câte ori am lucrat cu corpurile geometrice, copiii m-au întrebat dacă nu am și o sferă, să vedem cum se desface. Din păcate, setul nu o are, am compensat-o cu globuri din acelea transparente care se deschid sau cu mingiuțe. Le-am arătat un documentar despre cum se confecționează globurile geografice și cum e nevoie să fie decupată harta ca să fie lipită pe o sferă. Am tăiat o minge de plastic (din aceea de la piscinele cu bile) și am desfășurat-o relativ, arătându-le că aceste felii ca de pepene nu pot fi perfect întinse. Așadar nu vom putea face niciodată o sferă perfectă din hârtie.

Folding Geometric Shapes – EduClass: piesele principale desfășurate.

Când se recomandă?

Fără nici cea mai mică problemă, setul poate fi dat copilului de la orice vârstă la care înțelege că nu e o jucărie de spart. Chiar e păcat de el. Și, deși aveți impresia că nu va fi scos din cutie decât două-trei săptămâni pe an, în fiecare an școlar, efectele pe care el le va produce se vor vedea încet, în timp.

Iar dacă deja îl aveți, nu ezitați să îl puneți în ghiozdan când vedeți pe manual că urmează lecția despre corpuri. Ori profitați să îl oferiți în locul unui aranjament floral sau legat cu șnur de mărțișor, cu siguranță va produce mult mai multă bucurie dacă destinatarul este o persoană implicată și dornică să transforme experiențele de învățare oferite copiilor.

Setul este disponibil aici: EduClass

Alte variante:

Aflarea numărului necunoscut în clasele primare – bune practici pentru părinți (și nu numai)

Manualul pe care l-am folosit anul acesta la clasa întâi a plasat acest conținut dificil spre finalul anului școlar, nu la început, cum am văzut prin altele. Avantajele sunt destule, căci am avut timp suficient să abordăm proba adunării și scăderii, să rezolvăm probleme simple, care se reduc, în cele din urmă, la aflarea numărului necunoscut.

Însă distracția abia acum începe, mai ales când ai parte la clasă și de copii care regretă încă faptul că nu s-au născut învățați și, cum dau de greu, lasă lacrimi de crocodil să inunde foile, poate-poate dispar și cerințele. Și dacă la școală mai e cum mai e, acasă… e jale.

În primul și în primul rând, frustrarea copiilor e repede rezolvată de părinți. Ce-o fi găsit-o și pe-aia să facă ecuații la clasa întâi?? Încă n-am auzit-o și live, doar am citit-o pe grupuri de părinți înfuriați la culme că, uite, se îneacă cei mici în ecuații și nu pricep nimic nici când le explică ei, „de ce s-o face așa ceva la școală“?

De ce?

Pentru că… numărul necunoscut e parte din viața noastră.
Ce rest trebuie să primești la magazin dacă cumperi cu o bancnotă de 50 lei o carte de 35?
Dacă în pușculiță ai 17 lei, de câți lei mai ai nevoie pentru a cumpăra aceeași carte?

Primul sfat când vrei să ajuți copilul e să deschizi manualul, ca să nu dai explicații de gimnaziu unui copil din clasele primare. Nu neapărat manualul tipărit, ci cel digital. Cel puțin în al meu există un mod simpăticuț, ca să nu zic altfel, de a explica metoda balanței pentru aflarea numărului necunoscut. Privind derularea imaginilor, îmi dădeam seama de ce e atât de complicat totuși pentru copii să înțeleagă: poate și pentru că, de niște ani buni (un deceniu cu siguranță), nu o mai vezi la piață pe tanti Mița punând greutăți pe talerele cântarului în timp ce tu privești interesat cele două ciocuri de păsări echilibrate, să nu „te fure la cântar“. Acum… cântarul e electronic.

Chiar și jocurile de copii au astfel de instrumente, nu mai vezi o balanță de doamne-ajută, să se joace așa, cam de pe la 4 ani, să înțeleagă principiul echilibrului și dezechilibrului, cum „pui“ și cum „iei“ ca să le „egalezi“. Ei, dar lasă, au console, tablete și telefoane, la ce le folosește să se joace atâta? Fac mizerie cu nisip!

Am făcut primul pas

Sau l-am ignorat. Trecem mai departe… la introducerea în materialele auxiliare a literelor cu rol de necunoscută, care clar dau apă la moară celor care susțin că facem ecuații. Dacă scrii cu litere, așa este. Dar e mai ușor, nu? De ce să desenezi o căsuță goală? Sau să pui un semn al întrebării? Ori o floricică, un smiley…

Orice exercițiu de forma 🙂 + 5 = 12 capătă imediat sens dacă îl „citești“: la ce număr adunăm 5 și obținem 12?

Alte exemple:

? + 8 = 15 … Cu cât îl adunăm pe 8 să obținem 15? Cu 15 – 8.

19 – ? = 9 … Cât scădem din 19 pentru a rămâne cu 9?

? – 13 = 7 … Din ce număr scădem 13 pentru a obține 7?

Se pare că așa merge mult mai bine, dar… greu la deal cu boii mici, la matematică e dăunător sănătății să vorbești. Când ieși la tablă, taci ca peștele, nu cumva să deschizi gura. Verbalizarea procesului grăbește înțelegerea și pentru asta ne înarmăm cu un clește ca să scoatem cuvintele și ne luptăm în același timp cu încăpățânarea copiilor, care au impresia că, dacă nu fac în gând, nu sunt suficient de isteți. Aaa, și ferească Sfântul să le ceri să scrie și cum au aflat rezultatul, nu doar să completeze pătrățica liberă. „Dar de ce? Că am găsit răspunsul!“
Ei bine, uite de-asta! Pentru că nu răspunsul mă interesează neapărat, ci drumul până acolo.

Greșeli…

În ultimul timp, lucrând constant și cu copii mai măricei (a treia și a patra), mă apucă toate cele când îi aud că „trecem numărul dincolo cu semn schimbat“. Care semn?! Mulțimea numerelor naturale nu are semne… are operații de adunare și scădere, ca să nu mai zic că semnul schimbat al înmulțirii nu este cel de împărțire. În mulțimea numerelor naturale, nu avem ce să schimbăm și nici ce să trecem dintr-o parte într-alta a egalului.

Și totuși, o facem, dar cu explicații ce în primă fază par o scărpinătură oltenească. Folosești proba adunării și scăderii, proprietăți ale egalităților și, în cele din urmă, târziu, metoda mersului invers, pe care mulți le-au uitat după ce au învățat să rezolve algebric dileme ce le dădeau existența peste cap.

În încheiere, adaug ceea ce tatăl meu mi-a spus mereu: reușita e 1% inspirație și 99% transpirație. La matematică nu poți înțelege dacă nu stai cu creionul în mână. Un algoritm se învață când e repetat de un număr suficient de ori (pentru un copil oarecare, undeva în jur de 20). Aud atât de mult că nu mai „tocim“, formăm competențe. Ca să fii competent, întâi înveți (mult, dar și bine, să ai cunoștințele necesare), exersezi, capeți deprindere, ajungi la un algoritm de rezolvare și ai o abilitate. Toate împreună definesc o competență, pe care o vei forma în timp, cu multă muncă și sudoare, plus dorință de a reuși.

Fulgii de nea cad repede pe acest drum, nu rezistă. Vor, dar nu prea au strategia necesară.

La magazin – joc de pandemie

A doua primăvară cu restricții. Cea trecută – eram în online, la clasa pregătitoare, când am discutat despre leul românesc și despre finanțe, iar anul acesta, deși suntem la școală, restricțiile ne cam limitează creativitatea. În plus, atunci nici nu prea aveai cum să obligi părinții să se joace de-a magazinul cu copiii de 6 ani, deja prea mult ținuți în casă și plictisiți. M-am uitat în arhive, 40% din efectivul clasei au rezolvat cerința și au trimis o mică „dovadă“ a muncii depuse. Am insistat să se joace cu bani reali, să îi vadă, să îi simtă.

Apropo de bani reali, acum am discutat la școală că trebuie musai spălați dacă ne jucăm cu ei, căci nu știm în ce condiții i-au ținut posesorii lor de dinainte. Doamna, noroc că avem bani de plastic!! Da, cam așa…

După un an… clasa întâi

Prima lecție despre Leu a avut loc tot online. Am profitat, am cerut să aibă fiecare bancnote și monede spălate, să le studieze de aproape, să vedem ce culoare au și ce desene (detalii și explicații aici). Cel mai mult ne-a dat bătăi de cap Aurel Vlaicu, singurul la care desenatorul a scris numele cu alt font decât cel cu are copiii sunt obișnuiți. Nu l-au putut citi. Dar, ca la orice lecție online, dacă nu e și un părinte care să ajute, că „ăla e Traian Vuia“, nu avea haz.

Până la urmă am deslușit scrierea. Am aflat despre fiecare câte ceva. Iorga – istoric, Enescu – „muzicant“, de-asta avea note muzicale (compozitor și interpret li s-a părut că sună complicat), Grigorescu – pictor (a fost simplu, deja s-au prins că au indicii, pensula), Aurel Vlaicu – inventator, Caragiale – tatăl lui Ionel Popescu și al lui Goe, scriitor, dramaturg e complicat la clasa întâi.

După ce ne-am jucat un pic online pe Școala Intuitext, să plătim nota la restaurant, am avut ca temă o sarcină grea: aceea de a cheltui un leu, respectiv 100 de lei. A mai crescut un pic procentul de implicare, la 70% din colectiv, dar poate și pentru că în clasa întâi temele sunt luate ceva mai în serios. Oricum, nu sunt obligatorii, de ce să îți bați capul?!

Imagini – eMag

Am continuat joaca și la școală, cu un magazin mai aproape de sufletul meu, cu cărți, o activitate mai complicată în care am combinat aritmetica cu organizarea datelor în tabele, cu orientarea în spațiu, dar și cu lectura, căci povesteau repede ce cărți au acasă, ce-au citit, ori cereau detalii despre altele pe care nu le cunoșteau. Foarte isteți, s-au prins repede că la 6-8 lei e o carte subțire, așadar ușor de citit…

Lecția s-a încheiat cu un magazin. Cum interzicerea schimbului de obiecte făcea imposibil un magazin cu jucării aduse de-acasă, cu etichete și lei de hârtie, le-am cerut să deseneze pe o foaie jucăria pe care ar pune-o în vânzare, apoi am scris prețurile pe tablă. Dezamăgire maximă că nu pot vinde tablete și console cu sute de lei decât anul viitor, când socotim până la 1000, dar i-am lăsat să combine cum doresc, astfel încât să cheltuiască 100 lei.

În ordine: tabletă, creion, PS4, pușcă, sabie, cort, Barbie cu aragaz, minge, consolă cu jocuri, casă pentru păpuși, tablou cu autograf, mașinuță, țintă, piniata.

La final, când priveam colecția (pe care nu m-a lăsat inima să o strâng), mi-am amintit cum ne jucam demult, toată gașca de la bloc, de-a magazinul, cu bancnote din frunze, cu valoare după mărime, „ștampilate“ cu vreo jucărie cu rol de sigiliu BNR, cumpărând, cu ajutorul unui cântar improvizat dintr-o pârghie, făină, orez (nisip fin sau pietricele) ori te-miri-ce-altceva. Acum te poți juca cu un cântar adevărat, chiar electronic, la supermarket găsești legume de plastic și bani tipăriți, dar… rar mai vezi gașca de la bloc lăsată liberă să-și inventeze singură jocurile și jucăriile. Acolo exersam toată vacanța aritmetica de bază și aplicam ceea ce învățasem despre unitățile de măsură. Dar aceea e copilăria altor timpuri…

Operații cu puteri. Compararea puterilor

Compararea puterilor care nu au nici aceeași bază și nici același exponent reprezintă o încercare deosebită pentru rezolvitori, mai ales dacă aceștia sunt abia la începutul claselor gimnaziale, iar operațiile cu puteri sunt pentru ei o noutate absolută.

Acestea se pot însă duce la capăt prin diverse artificii de calcul, ceea ce înseamnă că ne vom folosi de operațiile învățate și de proprietățile lor pentru a obține în final o formă a exercițiului utilă în formularea răspunsului. Aceasta înseamnă că deprinderile de calcul și cunoașterea proprietăților operațiilor învățate trebuie stăpânite foarte bine, achiziții cu care elevul trebuie să vină din ciclul primar.

Așadar, pentru a compara două puteri care nu au nici aceeași bază și nici același exponent, ne vom strădui ca prin aceste artificii, folosind și proprietățile abia învățate ale puterilor, să le aducem la o formă asemănătoare. Cele două variante posibile sunt:

să aibă aceeași bază, ceea ce se poate, la exerciții mai simple, dacă bazele sunt puteri ale aceluiași număr.

Exemplu: Comparați puterile 2⁸ și 4⁷.

Putem scrie 2⁸=2^2·4 = (2²)⁴ = 4⁴ ; 4⁴ < 4⁷

Sau putem scrie 4⁷=(2²)⁷ = 2¹⁴; observăm că au aceeași bază, 8 < 14, înseamnă că 2⁸<2¹⁴, și, implicit, 2⁸<4⁷

să aibă același exponent.

Exemplul 1: Comparați puterile 2³⁶ și 3²⁴.

Observăm că nu au nici aceeași bază, nici aceiași exponenți. Pentru a realiza ceva asemănător, ne concentrăm atenția către exponenți. Putem scrie ca produs 36=3·12, iar 24=2·12 (Din păcate, la clasa a cincea capitolul despre divizibilitate urmează, de regulă, după cel dedicat operațiilor cu puteri, și copiilor le este dificil să descompună astfel numele, căci aceste deprinderi de lucru nu intră în programa ciclului primar. Pentru cei care știu divizibilitate, se caută cel mai mare divizor comun – cmmdc – al exponenților.)

2³⁶=2^(3·12) =(2³)¹²=8¹² (1)

La fel procedăm și în cazul următoarei puteri:

3²⁴ = 3^(2·12) = (3²)¹²=9¹² (2)

Din expresiile (1) și (2) putem trage următoarea concluzie: deoarece 8<9 => 8¹²< 9¹² , ceea ce înseamnă și că 2³⁶ < 3²⁴.

Exemplul 2: Comparați 4³³ și 3⁴⁴.

Observăm că 33 = 3·11, iar 44 = 4·11 (sau cmmdc=11).

4³³=4^(3·11) = (4³)¹¹ =64¹¹ (1)

3⁴⁴=3^(4·11)=(3⁴)¹¹=81¹¹ (2)

Din expresiile (1) și (2) putem concluziona că, deoarece 64<81, atunci și 64¹¹< 81¹¹, ceea ce înseamnă că 4³³ < 3⁴⁴.

Pentru a dobândi însă deprinderi și abilități de lucru cu puteri este însă necesar un exercițiu îndelungat, rezolvarea a multe exemple astfel încât să se formeze „ochiul“, adică să deprindă algoritmii posibili pentru a duce la bun sfârșit o astfel de provocare. Operațiile cu puteri vin însă pe fondul unei adaptări dificile a copilului de 10-11 ani la orarul de gimnaziu, cu solicitări masive de modelare a comportamentului pe cerințele complet diferite ale fiecărui profesor. De la abordarea prin joacă a tuturor noțiunilor aritmetice în clasele primare, face acum un salt uriaș la lucrul cu șiruri lungi de cifre, întinse pe caiete studențești.

Recomandăm utilizarea la clasă a exemplelor simple, pentru a încuraja copii, și mai puțin direct a celor de nivel olimpic, care nu fac decât să crească nivelul de frustrare și să-i determine să abandoneze cursa matematicii chiar înainte să vadă cât de spectaculoasă este aceasta.

Numerația 11-20: consolidare

Lecțiile de matematică au devenit mai complicate când, dincolo de scrierea și citirea numerelor din concentrul 11-20, am trecut la exerciții mai complicate, de ordonare și comparare. Unul din jocurile de încălzire cu care încep lecțiile este acela de a ordona pe axă numerele. Materialul l-am pregătit la începutul anului, l-am plastifiat, i-am adăugat pe spate bucățele de magnet și le pot așeza ușor pe tablă. De obicei desenez axa, pun marcajele și apoi împart jetoanele copiilor care trebuie să numere să vadă unde așază, căutând întâi cine îl are pe cel mai mic. Mai am o variantă, care presupune pe sfoară și prins cu cleme, dar nu am apucat să o fac doar cu numerele până la 10.

După ce le ordonăm, le citim în ordine crescătoare, apoi descrescătoare. Mutăm deasupra axei numerele pare (sau impare, nu contează, cât timp unele sunt deasupra, unele dedesubt) și le citim doar pe acestea, crescător și descrescător. Deja marea majoritate s-au obișnuit și le facem repede. Ultima dată am apucat să rezolvăm și exerciții de comparare a două numere, sau să stabilim vecinii unui număr, care e mai mare și care e mai mic.

Din păcate, cam aici ne-am oprit cu lecțiile. Pentru că pentru unii este încă dificil, am refăcut materialul de toamna trecută, l-am micșorat pentru a se putea utiliza mai ușor pe masă sau pe covor. Am scris numerele de la 0 la 20, le-am și reprezentat cu biluțe. Materialul disponibil aici se printează (preferabil pe carton sau se plastifiază) și se decupează, astfel încât să existe jetoane cu numere și jetoane cu mulțimi. Variante de joc:

Se amestecă jetoanele cu numere, se cere copilului să le ordoneze crescător / descrescător.
După așezarea numerelor, realizează corespodența între acestea și cartonașele cu mulțimi, prin numărarea elementelor.
Se cere să aleagă numele pare/impare și să le ordoneze crescător / descrescător.
Se extrage un număr și se cere copilului să găsească vecinii acestuia, să stabilească care e mai mare, care e mai mic.
Se extrag două numere și se compară, care e mai mare, care e mai mic.
Se caută numere mai mari decât x și mai mici decât y, în intervalul dat. Aici este de ajutor să se reașeze toate cartonașele în ordine crescătoare. Se mai pot cere numerele aflate între două numere date, sau de la un număr dat până la altul.

Fiecare variantă de joc se repetă până se observă că nu mai întâmpină dificultăți. După jumătate de oră de lucru, cel mult 45 minute, o pauză e binevenită. Se pot relua exercițiile care au mers mai greu, dar cele noi se lasă pentru ziua următoare.

Mai jos aveți o secvență de joc cu materialul de la clasă:

Mai multe variante de exerciții cu jetoanele confecționate aveți mai jos. Toate cele propuse pot fi realizate cu jetoanele de la 0 la 20, eu am optat pentru separarea celor două intervale din două motive simple. Primul, căci poate fi folosit separat cel cu numere până la 10, al doilea, ceva mai practic, nu îmi intra în cadru tot șirul de 21 de jetoane. Nu am inclus în video exercițiile de tipul „care sunt numerele mai mari decât … și mai mici decât…”, dar se pot realiza. Ca ultim sfat, repetați jocurile până când copilul nu mai întâmpină dificultăți.

Pentru numerele de la o la 10, aveți aici suportul video.

Numerația 11-20 – aplicații practice (CP)

Vacanța aceasta forțată a picat cum nu se putea mai neinspirat din punct de vedere al lecțiilor de matematică la clasa mea pregătitoare. Tocmai începusem numerația de la 11 la 20, apucasem să lucrez câteva ore cu copiii, speram ca săptămâna aceasta să pot trece la adunare dacă erau la un nivel satisfăcător, dar… n-a fost să fie. Cu mulți dintre ei merge bine, însă mai e mult până departe.

Am început să lucrez pentru acest concentru încă din primele zile de școală, de la înviorarea de dimineață, care se încheie cu o serie de genuflexiuni, câte zece, pe care le număram diferit: de la unu la 10, de la 11 la 20, de la 21 la 31 (ha, aici s-au prins unii repede că e una în plus!). Ca să nu ne plictisim, variam, de la 15 la 25 sau cum mai voiau ei. Ideea era să învățăm, ca pe poezie, cum se pronunță corect numeralele, să nu avem cinșpe, ci cincisprezece. Știu că e greu, și eu mă surprind uneori pe scurtătură, dar măcar ne străduim. Nu ne-a ieșit încă. Apoi a fost calendarul, în fiecare zi, și scrierea datei, chiar dacă prin imitație.

Toate bune și frumoase, până când ne-am apucat efectiv de treabă. Să grupezi zecile nu a fost chiar atât de simplu, iar eu voiam să „vadă zecea unită“. Am legat creioanele cu elastice, astfel încât zece creioane (care formau o zece) să stea ușor împreună. Am numărat mărgele, le-am pus câte 10 în cofraje, am înșirat câte 10 mărgele pe sârmă plușată și țineam în mână o zece, am pus jetoane cu magnet pe tablă pentru mulțimi, am scos rigletele și am format numere, am făcut mulțimi de câte 10 elemente pe hârtie. Sunt copii care au înțeles ușor, sunt destui care, cu insistențe, vor reuși, și sunt unii pentru care nu știu câte exerciții vor fi necesare, cât efort de concentrare, pentru că ei nu înțeleg de ce vin la școală și care sunt regulile aici.

Ce poți să faci să „înțelegi“ numerele până la 20 (asta în speranța că accepți faptul că a le recita ca pe poezie, corect, nu e același lucru cu înțelegerea conceptului):

îi dai copilului un număr de creioane (între 11 și 20), și îi ceri să formeze, prin numărare, mănunchiuri de câte 10. Câte mănunchiuri ai format? Câte creioane au rămas? Pentru a scrie numărul creioanelor, se notează întâi numărul de „mănunchiuri“ (adică numărul de zeci), apoi numărul de unități rămase. Se poate repeta cu orice tip de jucării sau obiecte mici, de la boabe de fasole la nasturi, piese lego. Important este ca o zece să fie izolată/încercuită, iar unitățile rămase în afară să fie cel mult 9, altfel se formează încă o zece.
pentru numerele identificate mai sus, se poate realiza corespondența cu riglette. „O zece“ există deja, este piesa cea mai lungă din set, se caută apoi piesa reprezentând numărul unităților dorite.
reprezentarea ordinelor pe numărătoarea pozițională este mai greu de explicat online. Eu le-am arătat copiilor prima dată cu bancnote. Am scos un mănunchi de bancnote de 1 leu, pe care ei le știu din viața de zi cu zi. Nimănui nu îi place să umble la el cu atâtea hârtii, să stai să numeri mereu câte ai. Așadar regula spune că pot schimba 10 hârtii verzi cu o hârtie roz. Ce valoare are o hârtie roz? Cât 10 hârtii verzi… Abia apoi am folosit numărătoarea pozițională. Dacă la unități am 10 bile, atunci am voie să le „schimb“ cu o bilă de la zeci. Am mers mult pe culori și 10 bile verzi fac cât o bilă roșie. Pe linia de la unități nu încap mai mult de 9, când se fac 10 – le transformăm. (Pentru că discurile de la numărătoarea pozițională sunt totuși mici, am improvizat una pe tablă, folosind discuri de carton cu magnet. Am lipit bandă izolieră colorată pentru suport, dar poză nu am făcut, din păcate. Seamănă însă cu cel folosind magneți de plastic, dar bulinele de carton au diametrul 7,5 cm.)

O activitate de acest gen, care să presupună multă joacă cu material concret, e mai utilă decât 20 de fișe de completat. Pentru exemplele fotografiate mai jos am lipit pe masă o folie de plastic (aceea folosită pentru a îmbrăca manualele) și scriu pe ea cu markere pentru tablă. Se șterge ok dacă insiști un pic și suplinește cu brio o tablă acasă. Dacă această variantă nu este posibilă, se poate plastifia un carton sau se poate folosi coală albă pe care se desenează mulțimile. La reutilizare, se plasează obiectele (10) în interiorul cercului desenat deja.

Pentru început am folosit buburuzele de lemn (cum spuneam, pot fi înlocuite cu orice obiecte), le-am grupat câte 10. Au rămas 3 în afara zecii. Corespondența am făcut-o cu riglette, o zece și trei unități. Apoi am folosit bețișoarele, am format o zece și trei unități. Am scris numărul 13, întâi cifra 1, reprezentând o zece – cifra zecilor – și apoi cifra 3, reprezentând unitățile – cifra unităților. Pentru a suplini numărătoarea pozițională, folosesc magneți (puteți folosi nasturi, buline decupate, biluțe din plastilină etc. sau se poate desena efectiv), un magnet roșu reprezintă o zece și este egală cu 10 unități (verzi). Același sistem l-am folosit și la clasele mai mari, am introdus albastrul pentru sute și apoi galben pentru mii. La clasa a patra, când am trecut la milion, nu mai era nevoie, reprezentam direct, fără a mai avea un cod de culori atât de strict.

Jocul se repetă pentru toate numerele, date pe sărite, nu consecutiv. Adultul care coordonează jocul este cel care dă copilului numărul de obiecte și urmărește corectitudinea rezolvării.

Dacă aveți și alte idei, completări sau întrebări, nu ezitați să le lansați mai jos, în comentarii.