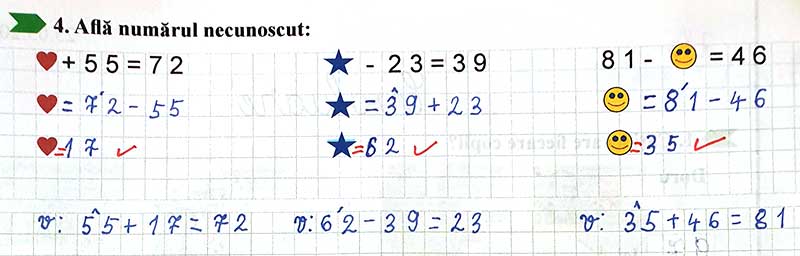Manualul pe care l-am folosit anul acesta la clasa întâi a plasat acest conținut dificil spre finalul anului școlar, nu la început, cum am văzut prin altele. Avantajele sunt destule, căci am avut timp suficient să abordăm proba adunării și scăderii, să rezolvăm probleme simple, care se reduc, în cele din urmă, la aflarea numărului necunoscut.
Însă distracția abia acum începe, mai ales când ai parte la clasă și de copii care regretă încă faptul că nu s-au născut învățați și, cum dau de greu, lasă lacrimi de crocodil să inunde foile, poate-poate dispar și cerințele. Și dacă la școală mai e cum mai e, acasă… e jale.
În primul și în primul rând, frustrarea copiilor e repede rezolvată de părinți. Ce-o fi găsit-o și pe-aia să facă ecuații la clasa întâi?? Încă n-am auzit-o și live, doar am citit-o pe grupuri de părinți înfuriați la culme că, uite, se îneacă cei mici în ecuații și nu pricep nimic nici când le explică ei, „de ce s-o face așa ceva la școală“?
De ce?
Pentru că… numărul necunoscut e parte din viața noastră.
Ce rest trebuie să primești la magazin dacă cumperi cu o bancnotă de 50 lei o carte de 35?
Dacă în pușculiță ai 17 lei, de câți lei mai ai nevoie pentru a cumpăra aceeași carte?
Primul sfat când vrei să ajuți copilul e să deschizi manualul, ca să nu dai explicații de gimnaziu unui copil din clasele primare. Nu neapărat manualul tipărit, ci cel digital. Cel puțin în al meu există un mod simpăticuț, ca să nu zic altfel, de a explica metoda balanței pentru aflarea numărului necunoscut. Privind derularea imaginilor, îmi dădeam seama de ce e atât de complicat totuși pentru copii să înțeleagă: poate și pentru că, de niște ani buni (un deceniu cu siguranță), nu o mai vezi la piață pe tanti Mița punând greutăți pe talerele cântarului în timp ce tu privești interesat cele două ciocuri de păsări echilibrate, să nu „te fure la cântar“. Acum… cântarul e electronic.
Chiar și jocurile de copii au astfel de instrumente, nu mai vezi o balanță de doamne-ajută, să se joace așa, cam de pe la 4 ani, să înțeleagă principiul echilibrului și dezechilibrului, cum „pui“ și cum „iei“ ca să le „egalezi“. Ei, dar lasă, au console, tablete și telefoane, la ce le folosește să se joace atâta? Fac mizerie cu nisip!
Am făcut primul pas
Sau l-am ignorat. Trecem mai departe… la introducerea în materialele auxiliare a literelor cu rol de necunoscută, care clar dau apă la moară celor care susțin că facem ecuații. Dacă scrii cu litere, așa este. Dar e mai ușor, nu? De ce să desenezi o căsuță goală? Sau să pui un semn al întrebării? Ori o floricică, un smiley…
Orice exercițiu de forma 🙂 + 5 = 12 capătă imediat sens dacă îl „citești“: la ce număr adunăm 5 și obținem 12?
Alte exemple:
? + 8 = 15 … Cu cât îl adunăm pe 8 să obținem 15? Cu 15 – 8.
19 – ? = 9 … Cât scădem din 19 pentru a rămâne cu 9?
? – 13 = 7 … Din ce număr scădem 13 pentru a obține 7?
Se pare că așa merge mult mai bine, dar… greu la deal cu boii mici, la matematică e dăunător sănătății să vorbești. Când ieși la tablă, taci ca peștele, nu cumva să deschizi gura. Verbalizarea procesului grăbește înțelegerea și pentru asta ne înarmăm cu un clește ca să scoatem cuvintele și ne luptăm în același timp cu încăpățânarea copiilor, care au impresia că, dacă nu fac în gând, nu sunt suficient de isteți. Aaa, și ferească Sfântul să le ceri să scrie și cum au aflat rezultatul, nu doar să completeze pătrățica liberă. „Dar de ce? Că am găsit răspunsul!“
Ei bine, uite de-asta! Pentru că nu răspunsul mă interesează neapărat, ci drumul până acolo.
Greșeli…
În ultimul timp, lucrând constant și cu copii mai măricei (a treia și a patra), mă apucă toate cele când îi aud că „trecem numărul dincolo cu semn schimbat“. Care semn?! Mulțimea numerelor naturale nu are semne… are operații de adunare și scădere, ca să nu mai zic că semnul schimbat al înmulțirii nu este cel de împărțire. În mulțimea numerelor naturale, nu avem ce să schimbăm și nici ce să trecem dintr-o parte într-alta a egalului.
Și totuși, o facem, dar cu explicații ce în primă fază par o scărpinătură oltenească. Folosești proba adunării și scăderii, proprietăți ale egalităților și, în cele din urmă, târziu, metoda mersului invers, pe care mulți le-au uitat după ce au învățat să rezolve algebric dileme ce le dădeau existența peste cap.
În încheiere, adaug ceea ce tatăl meu mi-a spus mereu: reușita e 1% inspirație și 99% transpirație. La matematică nu poți înțelege dacă nu stai cu creionul în mână. Un algoritm se învață când e repetat de un număr suficient de ori (pentru un copil oarecare, undeva în jur de 20). Aud atât de mult că nu mai „tocim“, formăm competențe. Ca să fii competent, întâi înveți (mult, dar și bine, să ai cunoștințele necesare), exersezi, capeți deprindere, ajungi la un algoritm de rezolvare și ai o abilitate. Toate împreună definesc o competență, pe care o vei forma în timp, cu multă muncă și sudoare, plus dorință de a reuși.
Fulgii de nea cad repede pe acest drum, nu rezistă. Vor, dar nu prea au strategia necesară.