Un tip de probleme care devin din ce în ce mai rare la ciclul primar sunt „problemele de viteză”, sau mai cunoscute ca probleme de mișcare. Înțeleg că sunt evitate, deoarece implică mărimi și noțiuni de fizică pe care copiii nu le au, dar pe care le pot totuși înțelege la această vârstă, pentru că s-au lovit constant de ele. Să luăm de exemplu noțiunea de „viteză”. O aude peste tot la tv, mai ales când accidentele țin în viață edițiile de știri. „Neadaptarea vitezei”, „viteză excesivă”, „depășirea limitei de viteză”. Primul lucru pe care îl reține este că viteza se măsoară în kilometri la oră.
Când am început să-i explic Irisucăi primele probleme de mișcare, i-am dat formula v=d:t. La un moment dat îmi spune că a memora așa, formule, e complicat, dar se gândește la kilometri la oră, că măsurăm distanța în kilometri, și ora este unitate pentru timp, și așa ține minte mai ușor. Așadar, are nevoie de asociere cu noțiuni pe care ea deja le-a înțeles/asimilat.
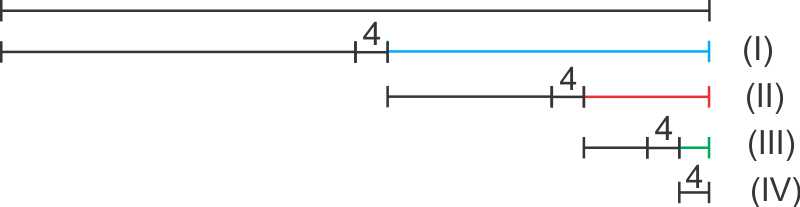
Problemele de mișcare trebuie însă pregătite cu un exercițiu de imaginație. Dacă nu-și va imagina problema, nu va putea să o rezolve, lectura textului fiind inutilă. Problemele de mișcare se împart în două mari categorii: prima – mobilele se deplasează în același sens (probleme de urmărire) și mobilele se deplasează în sens contrar (probleme de întâlnire). Se presupune din start că mobilele se deplasează în linie dreaptă, cu viteză constantă, și avem mișcare rectilinie și uniformă, altfel nu putem discuta de formula de mai sus, și nici rezolva problemele.
Acest articol este dedicat problemelor de urmărire.
Pentru a înțelege problemele, copilul trebuie să se gândească întâi, logic, dacă problema este posibilă, cu exemple.
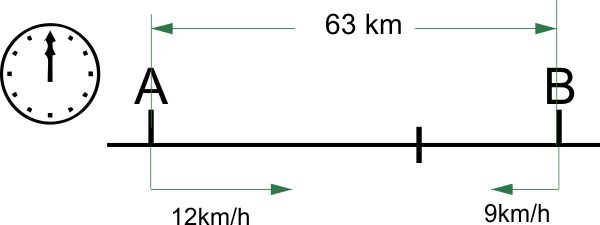
Orașele A și B se află pe aceeași șosea, la o distanță de 18 km unul de celălalt. Din orașul A pleacă spre orașul B la ora 12 un pieton. Din orașul B pleacă, în același sens, și la aceeași oră, un biciclist. La ce distanță de orașul A se întâlnesc cei doi, dacă pietonul se deplasează cu 3km/h, iar biciclistul cu 12km/h?
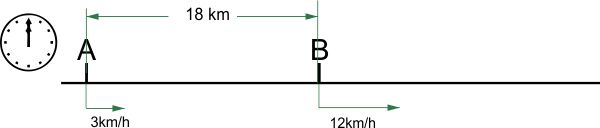
Dacă sărim la calcule, deja am pierdut problema din mână. Primul exercițiu care trebuie făcut este cel logic. Dacă biciclistul pleacă din orașul B, se apropie sau se depărtează de pieton? Are vreo șansă un om care merge pe jos să îl ajungă pe biciclist, care se deplasează mai repede decât el? Așadar, problema nu poate fi rezolvată (și cum materialele pentru elevi sunt pline de greșeli, exercițiul logic este obligatoriu).
Orașele A și B se află pe aceeași șosea, la o distanță de 18 km unul de celălalt. Din orașul A pleacă spre orașul B la ora 12 un pieton. Din orașul B pleacă, în același sens, și la aceeași oră, un alt pieton. La ce distanță de orașul A se întâlnesc cei doi, dacă pietonul din A se deplasează cu 3km/h, iar pietonul din B cu 3km/h?
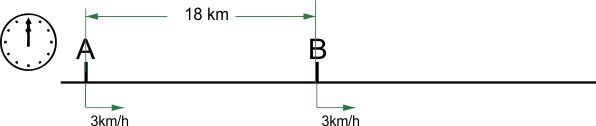
Folosind raționamentul de mai sus, stabilim că cei doi nu se vor întâlni niciodată, pentru că se deplasează cu aceeași viteză. Așadar – nici aici nu putem da un răspuns la întrebarea din problemă.
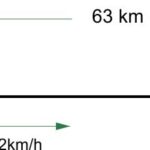
Orașele A și B se află pe aceeași șosea, la o distanță de 3km unul de celălalt. Din orașul A pleacă spre orașul B la ora 12 un biciclist . Din orașul B pleacă, în același sens, și la aceeași oră, un pieton. La ce distanță de orașul A se întâlnesc cei doi, dacă pietonul se deplasează cu 3km/h, iar biciclistul cu 12km/h?
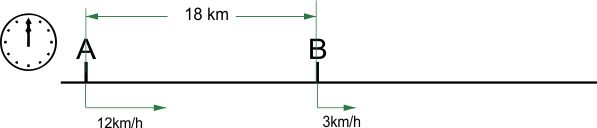
De data aceasta, stabilim că oricât de încet merge pietonul, biciclistul merge mai repede decât el, așadar la un moment dat îl va ajunge. Rămâne să aflăm când.
Am dat exemplele cu pieton și biciclist pentru a fi evident că unul se deplasează mai repede. Problemele pot avea diverse mobile, atenția trebuie să se oprească asupra vitezei cu care se deplasează acestea. Un alt aspect asupra căruia copilul trebuie să fie atent este ca unitățile de măsură să fie identice. În general acest tip de provocare este pentru clasele gimnaziale, dar nu se știe niciodată când viteza se exprimă în metri/secundă și este nevoie de transformări.
Revenind la ultima problemă, întâi trebuie să aflăm ce se întâmplă într-o oră.
12 – 3 = 9 ,
așadar, într-o oră, distanța dintre biciclist și pieton se micșorează cu 9 km, sau biciclistul este cu 9 km mai aproape de pieton.
Dinstanța dintre ei este de 18 km, și se micșorează cu 9 km în fiecare oră.
18 : 9 = 2
Două ore este timpul necesar pentru ca biciclistul să recupereze distanța dintre ei. În fiecare oră el recuperează 9km, așadar are nevoie de două ore pentru a recupera întreaga distanță.
Problema ne întreabă însă la ce distanță de A se vor întâlni cei doi. Putem afla răspunsul în două moduri:
I) Calculăm ce distanță parcurge pietonul în două ore – 3 x 2 = 6 (km) , și o adunăm cu distanța dintre cele două localități – 6 + 18 = 24 (km) . Așadar, se întâlnesc la 24 km distanță pe șosea de localitatea A.
II) Calculăm ce distanță parcurge în două ore biciclistul, care pleacă din A – 2 x 12 = 24 (km), și aflăm direct răspunsul final.
Este recomandabil să încurajați copilul să descopere ambele moduri de rezolvare, se poate verifica, și în același timp dobândește flexibilitate în gândire, toleranță față de opiniile celorlalți. Pot avea dreptate doi oameni, chiar dacă nu au mers pe același drum.
Problemele de urmărire pot avea și alte variante: cele două mobile pleacă din același punct, dar la ore diferite, și atunci trebuie să aflăm unde, la ce distanță de punctul de plecare se află primul mobil, atunci când pornește al doilea. Modelul de mai sus este forma la care se reduce orice problemă de urmărire pentru a fi rezolvată, iar algoritmul este următorul:
- se stabilește dacă „urmăritorul” îl poate ajunge pe urmărit.
- se află cu cât se micșorează distanța dintre cei doi în unitatea de timp
- se calculează în câte unități de timp poate fi recuperată distanța dintre cei doi în momentul în care se pun în mișcare.
Dincolo de acestea, mare atenție ce anume cere problema: să se afle distanța față de punctul de plecare, ori față de un punct intermediar de pe traseu care trebuie calculat.
Dacă v-ați lovit de probleme de mișcare ce v-au dat bătăi de cap, adaugați-le mai jos, împreună cu raționamentul/încercările de rezolvare eșuate, și vom încerca să le rezolvăm împreună. Menționez că nu este un articol ce-și propune să rezolve temele elevilor. Matematica este 1% inspirație și 99% transpirație. Cu inspirația am dat o mână de ajutor mai sus.