Există deja aici pe blog un articol despre metoda figurativă, varianta cunoscută de toată lumea – cu segmente. Însă sunt și probleme la care, oricât ne-am strădui, nu vom reuși să reprezentăm astfel suficient de clar datele pentru a fi pe înțelesul copiilor (clasa a IVa). Iată o astfel de problemă, și un model de rezolvare:
O familie cu copii are de 4 ori mai multe caiete dictando decât caiete de matematică.
După ce fiecare copil primește câte 2 caiete de matematică și 3 de dictando, rămân 2 caiete de matematică și 43 de dictando.Câte caiete și câți copii sunt ?
Pentru a ușura scrierea, voi nota în continuare cu M caietele de matematică și cu D caietele dictando.
Prima tendință în rezolvare este de a reprezenta cu segmente datele cunoscute ale problemei:
|____________| – caiete matematică
|____________|____________|____________|____________| – caiete dictando
Însă această reprezentare nu ne ajută la această problemă, când caietele sunt redistribuite. Așa că le vom așeza ca mai jos, atribuind fiecărui caiet de matematică patru caiete dictando, căci sunt de 4 ori mai multe.
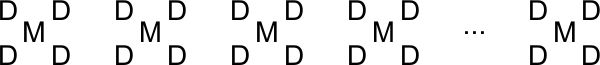
În acest moment am reprezentat toate caietele M și toate caietele D, care formează împreună grupuri, și avem de 4 ori mai multe D decât M.
Însă problema spune că aceste caiete sunt reorganizate, astfel încât fiecare copil primește 2 M și 3 D. Vom forma grupuri în care includem Acest număr de caiete, și observăm că, dacă luăm câte două grupuri inițiale, avem două caiete M, dar 8 caiete D.
Ca să rămânem cu 3, cum se specifică, trebuie să înlăturăm
8 – 3 = 5 (caiete D)

Am format grupuri similare numărului de copii din familie. Însă problema spune că rămân 2 caiete M și 43 D. Observăm că mai putem realiza un grup 2 M + 3 D, grup care nu va fi atribuit niciunui copil, dar acest lucru ne ajută să scăpăm de o necunoscută – caietele de matematică.

Unde „dispar” caietele D tăiate din grupurile inițiale? În dreapta, în cele 43 de caiete rămase.
Dacă mai formăm un grup de caiete (încadrat cu roșu), atunci vom avea:
43 – 3 = 40 (caiete D nedistribuite)
Raționamentul aici este următorul: avem 40 de caiete, care provin din X grupuri, și din fiecare grup câte 5. Din câte grupuri provin caietele?
40 : 5 = 8 (grupuri)
Dar aceste 8 grupuri nu reprezintă numărul copiilor, ci cu unul mai mult, căci noi am mai alcătuit un grup pe care nu l-am dat nimănui. Așadar, câți copii sunt în familie?
8 – 1 = 7 (copii)
Câte caiete M avem?
8 x 2 = 16 (caiete matematică)
Câte caiete D avem? (știm că sunt de 4x mai multe)
16 x 4 = 64 (caiete dictando)
Răspuns: 7 copii, 16 caiete matematică, 64 caiete dictando.
Succes!
Info: un copil normal, pentru a deprinde un algoritm de rezolvare, trebuie să îl exerseze de cel puțin 6-8 ori. Un copil cu dificultăți, până la 40 de ori.
- Daniel Pennac: Necazuri cu școala - 31 martie 2024
- Lecția despre piramidă - 30 martie 2024
- Dacii și romanii sau cum ne-am pomenit strămoșii - 17 martie 2024



Multumim pt idee, noua nu ne venise aceasta ingenioasa varianta de metoda grafica, ne tot straduiam sa gasim ceva cat mai explicit,sper sa functioneze mai bine asa!
Mai sunt două, tot cam așa, însă desenatul pentru pc nu e chiar atât de simplu de făcut.
Dacă tot le-am învățat la școală, să nu le țin doar pentru mine 🙂 .
Dar dacă sunt utile, mă voi strădui să-mi fac timp.
Foarte interesant!
Daca D = 4M, iar de fiecare data copiii ar fi primit caiete conform acestui raport , adica 2M si 8D, atunci ar fi ramas 2M si 8D. In realitate, fiecare copil a primit 2M si 3D, adica cu 5D mai putin. De asemenea au ramas efectiv 43, dar ar fi ramas 43-8 = 35D. Prin urmare, primind mai putine D decat raportul initial atunci raman D. Copiii primesc cu 5D mai putine si raman 35D, adica sunt 7 copii. 14 M si 56 M
Dacă sunt 7 copii, caietele de matematică sunt 16, deoarece fiecare copil primește două
7x 2 = 14,
dar mai rămân două caiete în plus, neatribuite niciunui copil.
Asadar, 16.